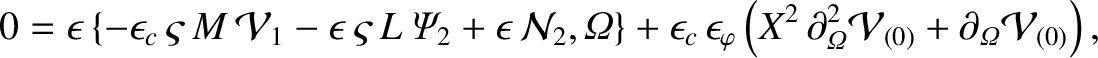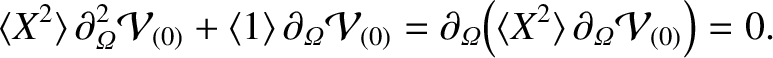Higher-Order Solution
In order to include the perpendicular transport term, we need to evaluate Equation (8.16) to third order in  . Doing so,
we obtain
. Doing so,
we obtain
 |
(8.77) |
where
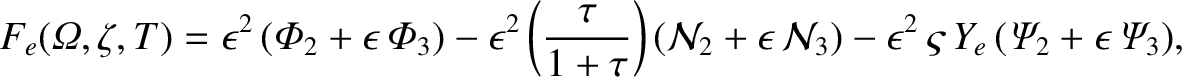 |
(8.78) |
and use has been made of Equations (8.49)–(8.53), (8.57), (8.58), (8.61), (8.62), and (8.75).
The flux-surface average of Equation (8.77) yields
 |
(8.79) |
where use has been made of Equations (8.68), (8.70), and (8.71). Hence, we
can write
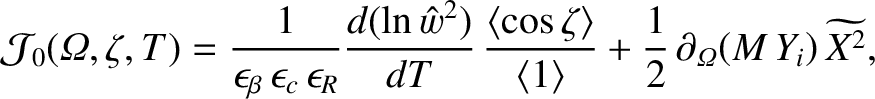 |
(8.80) |
where use has been made of Equation (8.76).
The first term on the right-hand side of the previous equation represents the parallel current driven
inductively when the reconnected flux at the rational surface varies in time.
The second term on the right-hand side of the previous equation represents the parallel return current driven by the perpendicular polarization current associated with the
acceleration of the ion fluid around the magnetic separatrix of the island chain [10,11].
In fact, it is easily seen that if the ion fluid could pass freely through the separatrix (i.e.,
 and
and
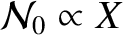 ) then the polarization term would be zero.
) then the polarization term would be zero.
In order to include the perpendicular transport term, we need to evaluate Equation (8.17) to first order in  . Doing so,
we obtain
. Doing so,
we obtain
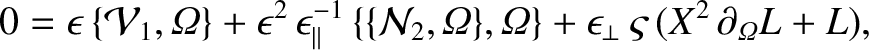 |
(8.81) |
where use has been made of Equations (8.49)–(8.53), (8.55), (8.57), and (8.58). The flux-surface average of the
previous equation yields
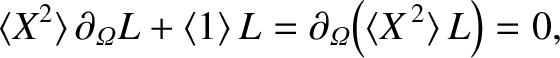 |
(8.82) |
where use has been made of Equation (8.68). Here, we have made use of the easily proved result that
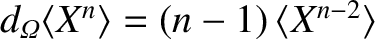 , where
, where
 .
We can solve the previous equation, subject to the boundary condition (8.59), to give
.
We can solve the previous equation, subject to the boundary condition (8.59), to give
![\begin{displaymath}L({\mit\Omega},T)= L({\mit\Omega})=\left\{
\begin{array}{llr}...
...5ex]
1/\langle X^2\rangle&~~&{\mit\Omega}>1
\end{array}\right..\end{displaymath}](img2848.png) |
(8.83) |
Here, we have taken into account the previously mentioned fact that 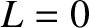 within the island separatrix.
within the island separatrix.
Note that
 is discontinuous across the island separatrix, which implies that the pressure gradient—and, hence,
the diamagnetic velocity—is also discontinuous across the separatrix. Of course, there is not a real
discontinuity. In fact, we would expect the discontinuity to be resolved in a layer on the separatrix whose width is obtained by balancing the
parallel and perpendicular energy transport terms in Equation (8.17) [3].
In other words, we expect the layer thickness to correspond to the island width at which
is discontinuous across the island separatrix, which implies that the pressure gradient—and, hence,
the diamagnetic velocity—is also discontinuous across the separatrix. Of course, there is not a real
discontinuity. In fact, we would expect the discontinuity to be resolved in a layer on the separatrix whose width is obtained by balancing the
parallel and perpendicular energy transport terms in Equation (8.17) [3].
In other words, we expect the layer thickness to correspond to the island width at which
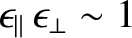 .
Hence, according to Equations (8.28) and (8.29), the characteristic layer thickness is
.
Hence, according to Equations (8.28) and (8.29), the characteristic layer thickness is 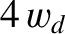 , where
, where
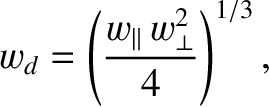 |
(8.84) |
and
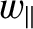 and
and 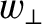 are specified in Equations (8.33) and (8.34), respectively. (The factor of 4 ensures that
are specified in Equations (8.33) and (8.34), respectively. (The factor of 4 ensures that
 has the same value as the standard critical island width,
has the same value as the standard critical island width, 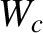 , defined
in Reference [3].)
As is clear from Table 8.1,
, defined
in Reference [3].)
As is clear from Table 8.1,  is of order half a centimeter in a tokamak fusion reactor.
is of order half a centimeter in a tokamak fusion reactor.
In order to include the perpendicular transport term, we need to evaluate Equation (8.18) to first order in  . Doing so,
we obtain
. Doing so,
we obtain
![$\displaystyle 0 =\epsilon\,\{{\cal J}_1,{\mit\Omega}\} +\epsilon_\varphi\,\vars...
...left[\partial_{\mit\Omega}\!\left(X^3\,\partial_{\mit\Omega} Y_i\right)\right].$](img2859.png) |
(8.85) |
where use has been made of Equations (8.49)–(8.53), (8.55), (8.57), (8.58), (8.61), (8.62), and (8.76). The flux-surface average of the previous equation yields
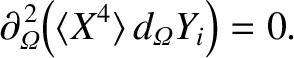 |
(8.86) |
We can solve the previous equation, subject to the boundary conditions (8.59) and (8.63), to give
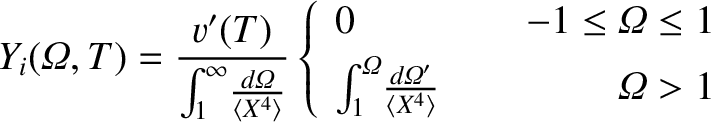 |
(8.87) |
[5].
Here, we have rejected, as unphysical, the solution that blows up as
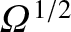 as
as
 .
We have also made use of the fact that
.
We have also made use of the fact that 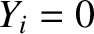 within the magnetic separatrix of the island chain. Finally, we have demanded that the ion
fluid velocity—and, hence, the function
within the magnetic separatrix of the island chain. Finally, we have demanded that the ion
fluid velocity—and, hence, the function
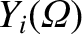 —be continuous across the separatrix, because the ion fluid possesses finite perpendicular viscosity.
Note, however, that the discontinuity in the function
—be continuous across the separatrix, because the ion fluid possesses finite perpendicular viscosity.
Note, however, that the discontinuity in the function
 across the island separatrix [see Equation (8.83)] implies that the
electron and MHD fluid velocities are discontinuous across the separatrix. (See Section 8.7.) As previously
mentioned, these discontinuities are resolved in a layer of characteristic thickness
across the island separatrix [see Equation (8.83)] implies that the
electron and MHD fluid velocities are discontinuous across the separatrix. (See Section 8.7.) As previously
mentioned, these discontinuities are resolved in a layer of characteristic thickness 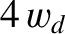 on the separatrix.
on the separatrix.
In order to include the perpendicular transport term, we need to evaluate Equation (8.19) to second order in  . Doing so,
we obtain
. Doing so,
we obtain
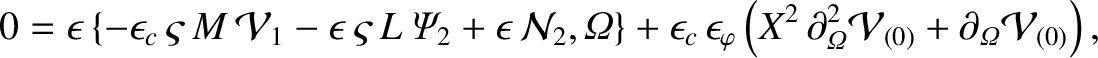 |
(8.88) |
where use has been made of Equations (8.49)–(8.53) (8.55), (8.57), (8.58), (8.61), (8.62), and (8.65). The flux-surface average of the
previous equation yields
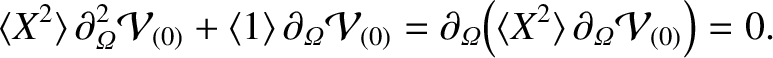 |
(8.89) |
The previous equation can be solved, subject to the boundary condition (8.43), to
give
 |
(8.90) |
Hence, we conclude that the lowest-order ion parallel flow is unaffected by the presence of the island chain.
 . Doing so,
we obtain
where
. Doing so,
we obtain
where
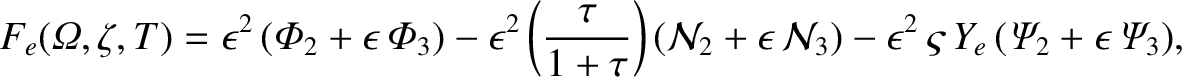

 and
and
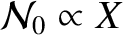 ) then the polarization term would be zero.
) then the polarization term would be zero.
 . Doing so,
we obtain
. Doing so,
we obtain
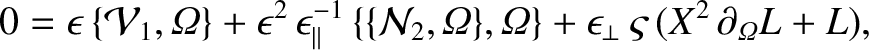
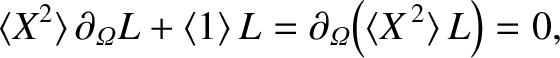
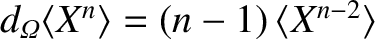 , where
, where
 .
We can solve the previous equation, subject to the boundary condition (8.59), to give
Here, we have taken into account the previously mentioned fact that
.
We can solve the previous equation, subject to the boundary condition (8.59), to give
Here, we have taken into account the previously mentioned fact that 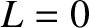 within the island separatrix.
within the island separatrix.
 is discontinuous across the island separatrix, which implies that the pressure gradient—and, hence,
the diamagnetic velocity—is also discontinuous across the separatrix. Of course, there is not a real
discontinuity. In fact, we would expect the discontinuity to be resolved in a layer on the separatrix whose width is obtained by balancing the
parallel and perpendicular energy transport terms in Equation (8.17) [3].
In other words, we expect the layer thickness to correspond to the island width at which
is discontinuous across the island separatrix, which implies that the pressure gradient—and, hence,
the diamagnetic velocity—is also discontinuous across the separatrix. Of course, there is not a real
discontinuity. In fact, we would expect the discontinuity to be resolved in a layer on the separatrix whose width is obtained by balancing the
parallel and perpendicular energy transport terms in Equation (8.17) [3].
In other words, we expect the layer thickness to correspond to the island width at which
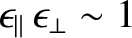 .
Hence, according to Equations (8.28) and (8.29), the characteristic layer thickness is
.
Hence, according to Equations (8.28) and (8.29), the characteristic layer thickness is 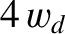 , where
, where
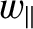 and
and 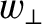 are specified in Equations (8.33) and (8.34), respectively. (The factor of 4 ensures that
are specified in Equations (8.33) and (8.34), respectively. (The factor of 4 ensures that
 has the same value as the standard critical island width,
has the same value as the standard critical island width, 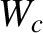 , defined
in Reference [3].)
As is clear from Table 8.1,
, defined
in Reference [3].)
As is clear from Table 8.1,  is of order half a centimeter in a tokamak fusion reactor.
is of order half a centimeter in a tokamak fusion reactor.
 . Doing so,
we obtain
. Doing so,
we obtain
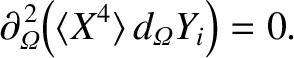
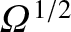 as
as
 .
We have also made use of the fact that
.
We have also made use of the fact that 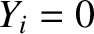 within the magnetic separatrix of the island chain. Finally, we have demanded that the ion
fluid velocity—and, hence, the function
within the magnetic separatrix of the island chain. Finally, we have demanded that the ion
fluid velocity—and, hence, the function
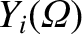 —be continuous across the separatrix, because the ion fluid possesses finite perpendicular viscosity.
Note, however, that the discontinuity in the function
—be continuous across the separatrix, because the ion fluid possesses finite perpendicular viscosity.
Note, however, that the discontinuity in the function
 across the island separatrix [see Equation (8.83)] implies that the
electron and MHD fluid velocities are discontinuous across the separatrix. (See Section 8.7.) As previously
mentioned, these discontinuities are resolved in a layer of characteristic thickness
across the island separatrix [see Equation (8.83)] implies that the
electron and MHD fluid velocities are discontinuous across the separatrix. (See Section 8.7.) As previously
mentioned, these discontinuities are resolved in a layer of characteristic thickness 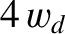 on the separatrix.
on the separatrix.
 . Doing so,
we obtain
. Doing so,
we obtain