Next: Fluid Velocities Up: Nonlinear Resonant Response Model Previous: Lowest-Order Solution Contents
 , is defined [8]
, is defined [8]
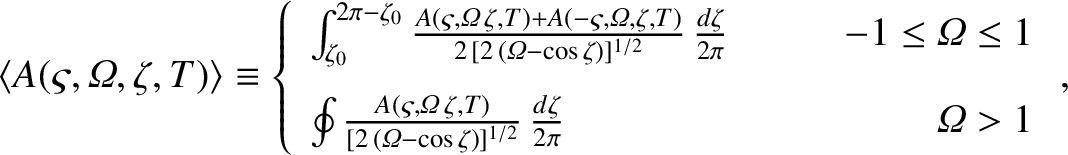 |
(8.67) |
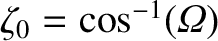 and
and
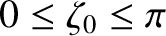 .
It follows that
for any
.
It follows that
for any
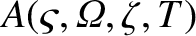 . It is helpful to define
. It is helpful to define
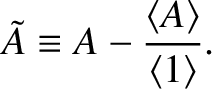 |
(8.69) |
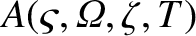 .
.
Equation (8.66) yields
where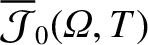 is an undetermined flux-surface function.
is an undetermined flux-surface function.