Next: Flux-Surface Average Operator Up: Nonlinear Resonant Response Model Previous: Ordering Scheme Contents
 , Equation (8.20) yields
, Equation (8.20) yields
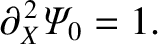 |
(8.54) |
 structure pictured in Figure 5.7. The island O-points correspond to
structure pictured in Figure 5.7. The island O-points correspond to
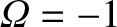 and
and
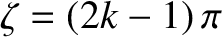 (where
(where  is an integer), the
X-points correspond to
is an integer), the
X-points correspond to
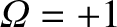 and
and
 , and the magnetic separatrix corresponds to
, and the magnetic separatrix corresponds to
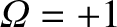 .
.
To zeroth order in  , Equation (8.19) yields
, Equation (8.19) yields
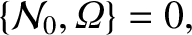 |
(8.56) |
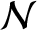 is an odd function of
is an odd function of 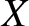 , it
follows that
We conclude that parallel
ion acoustic waves, whose dynamics are described by Equation (8.19), smooth out
any variations in the lowest-order normalized plasma pressure,
, it
follows that
We conclude that parallel
ion acoustic waves, whose dynamics are described by Equation (8.19), smooth out
any variations in the lowest-order normalized plasma pressure,
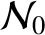 , around magnetic flux-surfaces [9].
By symmetry,
, around magnetic flux-surfaces [9].
By symmetry,
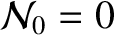 inside the magnetic separatrix of the island chain. In other words, the plasma pressure profile (and, by implication, the electron number density, electron temperature, and ion temperature profile—see Section 4.1) is completely flattened inside
the separatrix.
inside the magnetic separatrix of the island chain. In other words, the plasma pressure profile (and, by implication, the electron number density, electron temperature, and ion temperature profile—see Section 4.1) is completely flattened inside
the separatrix.
It is helpful to define
It follows that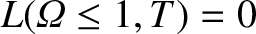 . Furthermore, Equations (8.41) and (8.55) imply that
. Furthermore, Equations (8.41) and (8.55) imply that
To zeroth order in  , Equation (8.16) yields
, Equation (8.16) yields
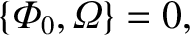 |
(8.60) |
 is an odd function of
is an odd function of 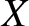 , it follows that
We conclude that the lowest-order normalized
MHD-fluid stream-function,
, it follows that
We conclude that the lowest-order normalized
MHD-fluid stream-function,
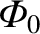 , is constant on magnetic flux-surfaces.
By symmetry,
, is constant on magnetic flux-surfaces.
By symmetry,
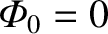 inside the magnetic separatrix of the island chain. In other words, the stream-function profile is completely flattened inside the separatrix.
inside the magnetic separatrix of the island chain. In other words, the stream-function profile is completely flattened inside the separatrix.
It is helpful to define
It follows that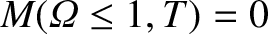 . Furthermore, Equations (8.42) and (8.55) imply that
. Furthermore, Equations (8.42) and (8.55) imply that
To zeroth order in  , Equation (8.17) yields
, Equation (8.17) yields
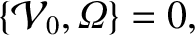 |
(8.64) |
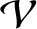 is an even function of
is an even function of 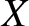 , we can write
In other words, the lowest-order normalized parallel ion velocity,
, we can write
In other words, the lowest-order normalized parallel ion velocity,
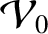 , is also constant on
magnetic flux-surfaces.
, is also constant on
magnetic flux-surfaces.
Finally, to zeroth order in  , Equation (8.18) yields
, Equation (8.18) yields
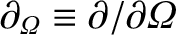 .
.