Next: Ordering Scheme Up: Nonlinear Resonant Response Model Previous: Reduced Drift-MHD Model Contents
 is the diamagnetic frequency at the rational surface [see Equation (5.47)], and
is the diamagnetic frequency at the rational surface [see Equation (5.47)], and
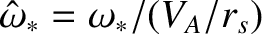 .
It follows that
.
It follows that
 in the immediate vicinity of the island chain.
in the immediate vicinity of the island chain.
It is helpful to define the
rescaled fields
 ,
,
 ,
,
 ,
,
 , and
, and
 , where
, where
 a dimensionless measure of the plasma pressure at the rational surface [see Equation (4.65)].
a dimensionless measure of the plasma pressure at the rational surface [see Equation (4.65)].
The reduced drift-MHD model specified in Section 5.2 rescales to give
Here,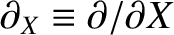 ,
,
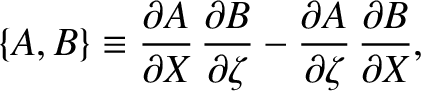 |
(8.21) |
 |
(8.22) |
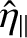 is the normalized parallel plasma resistivity at the
rational surface [see Equation (5.14)].
Furthermore,
where
Here,
is the normalized parallel plasma resistivity at the
rational surface [see Equation (5.14)].
Furthermore,
where
Here,
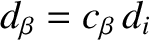 is the ion sound radius,
is the ion sound radius,  the resistive diffusion time [see Equation (5.49)],
the resistive diffusion time [see Equation (5.49)],
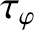 the toroidal momentum confinement time [see Equation (5.50)], and
the toroidal momentum confinement time [see Equation (5.50)], and
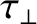 the energy confinement time [see Equation (5.52)]. All of these quantities are evaluated at the rational surface.
Moreover,
is the effective pressure gradient scale-length at the rational surface, and
the energy confinement time [see Equation (5.52)]. All of these quantities are evaluated at the rational surface.
Moreover,
is the effective pressure gradient scale-length at the rational surface, and
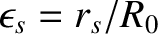 .
Finally,
where
.
Finally,
where
 |
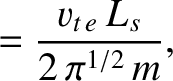 |
(8.37) |
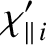 |
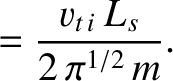 |
(8.38) |
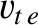 and
and  are the electron and ion thermal velocities, respectively [see Equation (2.17)].
Note that the parallel electron and ion energy diffusivities
have been estimated from Equations (2.319) and (2.320), respectively,
on the assumption that
are the electron and ion thermal velocities, respectively [see Equation (2.17)].
Note that the parallel electron and ion energy diffusivities
have been estimated from Equations (2.319) and (2.320), respectively,
on the assumption that
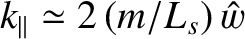 , which is the typical parallel wavenumber of the tearing perturbation at the edge of a magnetic island chain of reduced width
, which is the typical parallel wavenumber of the tearing perturbation at the edge of a magnetic island chain of reduced width  . Note that in writing Equation (8.18)
we have made use of the easily proved identity
. Note that in writing Equation (8.18)
we have made use of the easily proved identity
Equations (8.16)–(8.20) must be solved subject to the boundary conditions [see Equations (8.2)–(8.6) and (8.11)–(8.15)]
as . Here,
where
. Here,
where
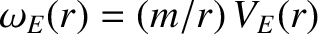 is the E-cross-B frequency profile.
Note that
is the E-cross-B frequency profile.
Note that
 ,
, 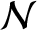 ,
,
 ,
, 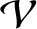 , and
, and  are all
are all
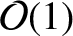 quantities in the inner region.
Note, further, that the boundary conditions (8.40)–(8.44),
as well as the symmetry of the rescaled, reduced, drift-MHD equations, (8.16)–(8.20), ensure that
quantities in the inner region.
Note, further, that the boundary conditions (8.40)–(8.44),
as well as the symmetry of the rescaled, reduced, drift-MHD equations, (8.16)–(8.20), ensure that
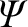 ,
, 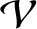 , and
, and
 are even functions of
are even functions of 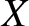 , whereas
, whereas 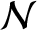 and
and
 are odd functions.
are odd functions.