Next: Rescaled Reduced Drift-MHD Model Up: Nonlinear Resonant Response Model Previous: Introduction Contents
 , (see Section 4.3) in our reduced drift-MHD model equal to the minor radius of the rational surface,
, (see Section 4.3) in our reduced drift-MHD model equal to the minor radius of the rational surface, 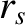 . The model evolves four scalar fields. These fields, which are defined in Equations (5.1)–(5.4), are the (normalized) helical magnetic flux,
. The model evolves four scalar fields. These fields, which are defined in Equations (5.1)–(5.4), are the (normalized) helical magnetic flux,  , the (normalized) perturbed total plasma pressure,
, the (normalized) perturbed total plasma pressure, 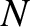 , the (normalized)
MHD fluid stream-function,
, the (normalized)
MHD fluid stream-function,  , and the (normalized) ion
parallel velocity,
, and the (normalized) ion
parallel velocity, 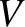 . The four fields, as
well as the auxiliary field,
. The four fields, as
well as the auxiliary field,  , which is defined in Equation (5.8), are assumed only to be functions of the normalized radial coordinate
, which is defined in Equation (5.8), are assumed only to be functions of the normalized radial coordinate
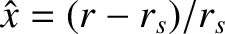 , the helical angle
, the helical angle
 , and the
normalized time
, and the
normalized time
 . Here,
. Here,  ,
,  ,
, 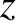 are conventional cylindrical coordinates,
are conventional cylindrical coordinates,
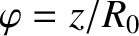 a simulated toroidal angle (see Chapter 3),
a simulated toroidal angle (see Chapter 3),  the simulated major radius of the plasma, and
the simulated major radius of the plasma, and 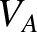 the Alfvén speed [see Equation (4.23)].
the Alfvén speed [see Equation (4.23)].
It is convenient to work in a frame of reference that co-rotates with the island chain. [This goal can be achieved by making the transformation
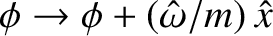 . See the following paragraph for the definitions of these quantities.] In the co-rotating reference frame, the
normalized reconnected flux at the rational surface,
. See the following paragraph for the definitions of these quantities.] In the co-rotating reference frame, the
normalized reconnected flux at the rational surface,
 [see Equation (3.184)], is assumed to be a positive real quantity. It is helpful to define the reduced (by a factor four) radial width of the magnetic island chain
that develops in the inner region:
[see Equation (3.184)], is assumed to be a positive real quantity. It is helpful to define the reduced (by a factor four) radial width of the magnetic island chain
that develops in the inner region:
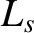 is the magnetic shear-length at the rational surface [see Equation (5.27)].
is the magnetic shear-length at the rational surface [see Equation (5.27)].
In the following, it is assumed that
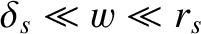 , where
, where  is the linear layer width. (See Chapter 6.)
In other words, the width of the island chain is assumed to be much greater than the linear layer width, but much less than the minor
radius of the rational magnetic flux-surface. Let
is the linear layer width. (See Chapter 6.)
In other words, the width of the island chain is assumed to be much greater than the linear layer width, but much less than the minor
radius of the rational magnetic flux-surface. Let
 . Reusing the analysis of Section 5.3,
we find that
. Reusing the analysis of Section 5.3,
we find that
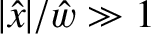 (i.e., many island widths from the rational surface).
Here,
(i.e., many island widths from the rational surface).
Here,
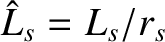 ,
,
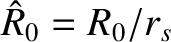 ,
,
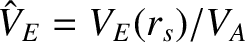 ,
,
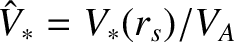 ,
,
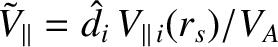 ,
,
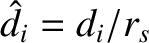 , and
, and
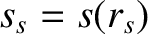 , where
, where  is the E-cross-B
velocity profile in the outer region [see Equation (5.21)],
is the E-cross-B
velocity profile in the outer region [see Equation (5.21)], 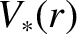 the diamagnetic velocity profile [see Equation (5.29)],
the diamagnetic velocity profile [see Equation (5.29)],
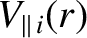 the ion parallel velocity profile [see Equation (5.19)],
the ion parallel velocity profile [see Equation (5.19)],
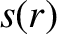 the magnetic shear profile [see Equation (5.28)], and
the magnetic shear profile [see Equation (5.28)], and 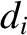 the collisionless ion skin-depth at the rational surface [see Equation (4.24)].
Moreover,
the collisionless ion skin-depth at the rational surface [see Equation (4.24)].
Moreover,
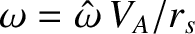 is the rotation frequency of the tearing mode in the
laboratory frame,
is the rotation frequency of the tearing mode in the
laboratory frame,
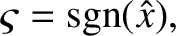 |
(8.7) |
![$\displaystyle \hat{V}_E' = \frac{1}{V_A}\left[r\,\frac{dV_E}{dr}\right]_{r_{s-}}^{r_{s+}}.$](img2638.png) |
(8.8) |
 is introduced into the analysis in order to take into account the fact that the E-cross-B velocity profile in the outer region develops a
gradient discontinuity at the rational surface in response to the localized electromagnetic torque that emerges
at the surface. Note, finally, that in neglecting any dependance of
is introduced into the analysis in order to take into account the fact that the E-cross-B velocity profile in the outer region develops a
gradient discontinuity at the rational surface in response to the localized electromagnetic torque that emerges
at the surface. Note, finally, that in neglecting any dependance of
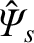 on
on 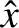 in Equation (8.2)
we are making use of the so-called constant-
in Equation (8.2)
we are making use of the so-called constant- approximation [7,8], which
is valid as long as
approximation [7,8], which
is valid as long as
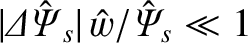 , where
, where
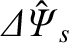 is defined in Equations (3.73) and (3.183) [2,4].
is defined in Equations (3.73) and (3.183) [2,4].