Next: Modification of Rotation Frequency Up: Cylindrical Tearing Mode Theory Previous: Plasma Angular Equations of Contents
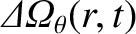 and
and
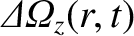 , are
localized in the vicinity of the rational surface [4]. Hence, it is reasonable to express the perturbed angular
equations of motion, (3.161) and (3.165), in the simplified forms
where
, are
localized in the vicinity of the rational surface [4]. Hence, it is reasonable to express the perturbed angular
equations of motion, (3.161) and (3.165), in the simplified forms
where
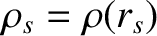 ,
,
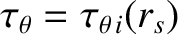 , and
, and
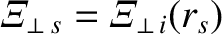 .
where
Here,
.
where
Here, 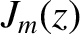 is a Bessel function, and
is a Bessel function, and  denotes its
denotes its  th zero [1]. Note that
Equations (3.170)–(3.173) automatically satisfy the boundary conditions (3.166) and (3.167).
th zero [1]. Note that
Equations (3.170)–(3.173) automatically satisfy the boundary conditions (3.166) and (3.167).
It is easily demonstrated that [13]
 |
 |
(3.174) |
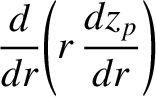 |
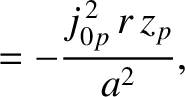 |
(3.175) |
 |
![$\displaystyle = \frac{a^{4}}{2}\,[J_2(j_{1p})]^{\,2}\,\delta_{pq},$](img1751.png) |
(3.176) |
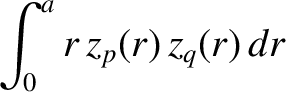 |
![$\displaystyle = \frac{a^{2}}{2}\,[J_1(j_{0p})]^{\,2}\,\delta_{pq}.$](img1753.png) |
(3.177) |
Equations (3.139), (3.140), and (3.168)–(3.177) yield
Here, is the momentum confinement time, is the Alfvén time, |
(3.182) |