Next: Tearing Mode Evolution Equations Up: Cylindrical Tearing Mode Theory Previous: Solution of Plasma Angular Contents
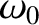 is the natural frequency of the tearing mode. The natural frequency is defined as the rotation frequency of tearing mode that develops
spontaneously, and does not interact with any external structure (such as a resistive wall or an error-field).
The previous expression is known as the no-slip constraint [4], and has been verified experimentally [12].
It follows from Equations (3.170)
and (3.171) that
is the natural frequency of the tearing mode. The natural frequency is defined as the rotation frequency of tearing mode that develops
spontaneously, and does not interact with any external structure (such as a resistive wall or an error-field).
The previous expression is known as the no-slip constraint [4], and has been verified experimentally [12].
It follows from Equations (3.170)
and (3.171) that