Next: Solution of Plasma Angular Up: Cylindrical Tearing Mode Theory Previous: Electromagnetic Torques Contents
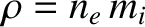 is the plasma mass density,
is the plasma mass density, 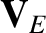 the E-cross-B velocity [see Equation (2.138)],
the E-cross-B velocity [see Equation (2.138)],
 the ion diamagnetic velocity [see Equation (2.139)],
the ion diamagnetic velocity [see Equation (2.139)], 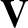 the MHD velocity [see Equation (2.321)],
the MHD velocity [see Equation (2.321)],
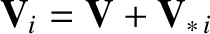 the ion fluid velocity,
the ion fluid velocity,
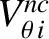 the neoclassical poloidal velocity [see Equation (2.330)],
the neoclassical poloidal velocity [see Equation (2.330)],
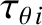 the poloidal
flow-damping time [see Equation (2.332)], and
the poloidal
flow-damping time [see Equation (2.332)], and
 the perpendicular ion momentum
diffusivity. In writing the previous equation, we have assumed that
the perpendicular ion momentum
diffusivity. In writing the previous equation, we have assumed that
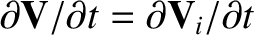 because changes in the ion fluid rotation induced by tearing modes are mostly due to changes in the MHD
velocity, rather than changes in the ion diamagnetic velocity (which is fixed by the ion pressure profile).
because changes in the ion fluid rotation induced by tearing modes are mostly due to changes in the MHD
velocity, rather than changes in the ion diamagnetic velocity (which is fixed by the ion pressure profile).
Now, according to the analysis of Section 2.25, the dominant terms in the previous equation are
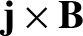 and
and 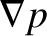 . However, if we either take the poloidal flux-surface integral,
. However, if we either take the poloidal flux-surface integral,
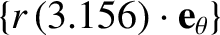 , or the toroidal flux-surface integral,
, or the toroidal flux-surface integral,
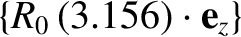 , of this equation then
the
, of this equation then
the 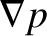 term is completely annihilated (because
term is completely annihilated (because  is a single-valued function of
is a single-valued function of  and
and  ), and
the
), and
the
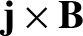 term is largely annihilated. In fact, as was demonstrated in the previous section,
the residual
term is largely annihilated. In fact, as was demonstrated in the previous section,
the residual
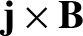 term is quadratic in perturbed quantities, and localized in the vicinity of the
rational surface. In these circumstance, it makes sense to include contributions from the other smaller terms in
Equation (3.156). We shall calculate these contributions using the lowest-order (i.e., neglecting the contribution of the tearing perturbation) ion flow,
term is quadratic in perturbed quantities, and localized in the vicinity of the
rational surface. In these circumstance, it makes sense to include contributions from the other smaller terms in
Equation (3.156). We shall calculate these contributions using the lowest-order (i.e., neglecting the contribution of the tearing perturbation) ion flow,
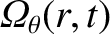 and
and
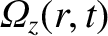 are the ion poloidal and toroidal angular
velocity profiles, respectively.
are the ion poloidal and toroidal angular
velocity profiles, respectively.
Taking
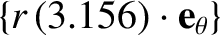 , where the flux-surface integration operator is defined in
Equation (3.131), we find that [11]
, where the flux-surface integration operator is defined in
Equation (3.131), we find that [11]
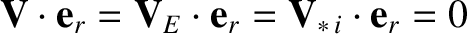 . Here,
. Here,
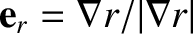 . Moreover,
. Moreover,
 . Here, we have added a
source term,
. Here, we have added a
source term,
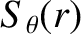 , to the previous equation in order to account for the equilibrium flow.
Let
, to the previous equation in order to account for the equilibrium flow.
Let
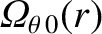 be the
unperturbed (by the tearing mode) ion poloidal angular velocity profile. It follows that
be the
unperturbed (by the tearing mode) ion poloidal angular velocity profile. It follows that
![$\displaystyle S_\theta = 4\pi^2\,R_0\left[ \frac{\rho}{\tau_{\theta\,i}}\,r^3\,...
...{\mit\Xi}_{\perp\,i}\,r^3\,\frac{d{\mit\Omega}_{\theta\,0}}{d r}\right)\right].$](img1712.png) |
(3.159) |
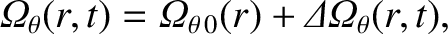 |
(3.160) |
 is the modification to the ion poloidal angular velocity profile
induced by the tearing mode, Equation (3.158)
yields [4]
is the modification to the ion poloidal angular velocity profile
induced by the tearing mode, Equation (3.158)
yields [4]
Taking
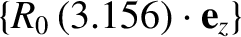 , we find that [11]
, we find that [11]
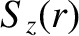 , to the previous equation in order to account for the equilibrium flow. Let
, to the previous equation in order to account for the equilibrium flow. Let
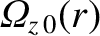 be the
unperturbed (by the tearing mode) ion toroidal angular velocity profile. It follows that
be the
unperturbed (by the tearing mode) ion toroidal angular velocity profile. It follows that
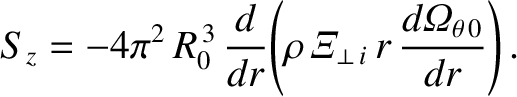 |
(3.163) |
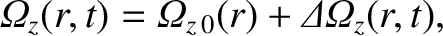 |
(3.164) |
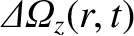 is the modification to the ion toroidal angular velocity profile
induced by the tearing mode, Equation (3.162)
yields [4]
is the modification to the ion toroidal angular velocity profile
induced by the tearing mode, Equation (3.162)
yields [4]
Equations (3.161) and (3.165) are subject to the boundary conditions
The boundary conditions (3.166) merely ensure that the ion angular velocities remain finite at the magnetic axis. On the other hand, the boundary conditions (3.167) are a consequence of the action of charge exchange with electrically neutral particles emitted isotropically from the wall in the edge regions of the plasma [2,4,8]. Charge exchange with neutrals gives rise to dominant damping torques acting at the edge of the plasma that relax the edge ion angular velocities toward particular values. Moreover, the electromagnetic torques that develop at the rational surface are not large enough, compared with the charge-exchange torques, to significantly modify the edge ion angular velocities [4].