Next: Reduced Drift-MHD Model Up: Nonlinear Resonant Response Model Previous: Nonlinear Resonant Response Model Contents
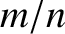 . Here,
. Here,  and
and 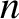 are the poloidal and toroidal mode numbers, respectively, of the tearing mode.
A radially thin region forms around the rational magnetic flux-surface, and
constitutes the inner region.
As was discussed in Section 5.16, the response of the plasma in the inner region to a rotating tearing perturbation in the outer region is accurately described by
linear theory only
when the width of the magnetic island chain that develops at the rational surface is less than the linear layer width.
In the opposite limit, in which the island width exceeds the layer width, a nonlinear approach is required.
The aim of this chapter is to employ the reduced drift-MHD model derived in Chapter 4 to determine the nonlinear response of the plasma in the inner region to a rotating tearing perturbation in the outer region.
are the poloidal and toroidal mode numbers, respectively, of the tearing mode.
A radially thin region forms around the rational magnetic flux-surface, and
constitutes the inner region.
As was discussed in Section 5.16, the response of the plasma in the inner region to a rotating tearing perturbation in the outer region is accurately described by
linear theory only
when the width of the magnetic island chain that develops at the rational surface is less than the linear layer width.
In the opposite limit, in which the island width exceeds the layer width, a nonlinear approach is required.
The aim of this chapter is to employ the reduced drift-MHD model derived in Chapter 4 to determine the nonlinear response of the plasma in the inner region to a rotating tearing perturbation in the outer region.