Next: Reduction Process Up: Reduced Resonant Response Model Previous: Drift-MHD Fluid Equations Contents
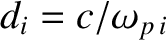 , where
, where 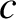 is the velocity of light in vacuum, and
is the velocity of light in vacuum, and
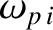 the ion plasma
frequency [2].
the ion plasma
frequency [2].
Let 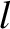 be a typical variation lengthscale in the resonant layer. It is convenient to adopt the following normalization scheme that renders all quantities in the drift-MHD fluid equations
dimensionless:
be a typical variation lengthscale in the resonant layer. It is convenient to adopt the following normalization scheme that renders all quantities in the drift-MHD fluid equations
dimensionless:
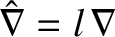 ,
,
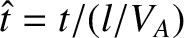 ,
,
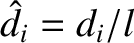 ,
,
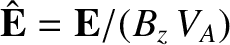 ,
,
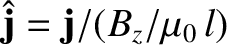 ,
,
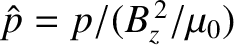 ,
,
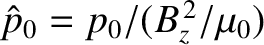 ,
,
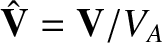 ,
,
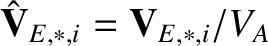 ,
,
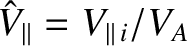 ,
,
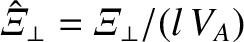 ,
,
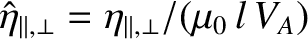 , and
, and
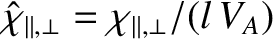 .
Equations (4.7)–(4.13) and (4.20)–(4.22) yield the following set of
normalized drift-MHD fluid equations:
.
Equations (4.7)–(4.13) and (4.20)–(4.22) yield the following set of
normalized drift-MHD fluid equations: