Next: Drift-MHD Fluid Equations Up: Reduced Resonant Response Model Previous: Reduced Resonant Response Model Contents
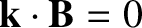 , where
, where 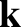 is the wavenumber of the tearing mode, and
is the wavenumber of the tearing mode, and 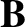 the equilibrium magnetic field. A radially thin resistive layer forms around the rational magnetic flux-surface, and
constitutes the so-called inner region. The tearing mode solution in the inner region needs to be asymptotically
matched to that in the outer region [5]. In principle, the relatively complicated neoclassical fluid equations, (2.370)–(2.374),
must be used to describe the resonant plasma response in the inner region. Note, however, that the set of tearing mode evolution equations, (3.187)–(3.191), derived in the previous chapter, only contains two quantities that actually depend on the
plasma response in the inner region: namely, the reconnection time,
the equilibrium magnetic field. A radially thin resistive layer forms around the rational magnetic flux-surface, and
constitutes the so-called inner region. The tearing mode solution in the inner region needs to be asymptotically
matched to that in the outer region [5]. In principle, the relatively complicated neoclassical fluid equations, (2.370)–(2.374),
must be used to describe the resonant plasma response in the inner region. Note, however, that the set of tearing mode evolution equations, (3.187)–(3.191), derived in the previous chapter, only contains two quantities that actually depend on the
plasma response in the inner region: namely, the reconnection time, 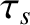 , and the
natural frequency,
, and the
natural frequency,
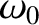 . This fact suggests that the true set of equations that describe the plasma response in the inner region are almost certainly considerably simpler than the neoclassical fluid equations. Let us search for some simplifying approximations.
. This fact suggests that the true set of equations that describe the plasma response in the inner region are almost certainly considerably simpler than the neoclassical fluid equations. Let us search for some simplifying approximations.
One simplifying approximation that we can make is to ignore the specifically neoclassical terms (e.g., the terms associated with ion poloidal flow damping and the bootstrap current) in the neoclassical fluid equations. As we
saw in Chapter 2, all of these terms have their origin in friction between trapped and passing particles.
However, trapped ions make radial excursions from magnetic flux-surfaces that are of order the ion banana
width,
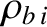 . (See Section 2.7.) As shown in Table 2.4, this width is a few centimeters in a tokamak fusion
reactor. In situations in which the width of the inner region is much less than the ion banana width, we would not
expect ion neoclassical effects to contribute to the plasma response in the inner region (because the trapped
ions would average over the spatial structure of the inner region). According to Table 2.4, the
electron banana width is of order a few tenths of a centimeter in a tokamak fusion reactor. Hence, we would not expect electron neoclassical
effects to contribute to the plasma response in very thin
resistive layers. When our neoclassical fluid equations are stripped of specifically neoclassical terms, we shall
refer to then as drift-MHD fluid equations. The “drift” appellation merely indicates that we are still taking diamagnetic flows into account, which necessarily entails treating the ion and electron flows separately.
. (See Section 2.7.) As shown in Table 2.4, this width is a few centimeters in a tokamak fusion
reactor. In situations in which the width of the inner region is much less than the ion banana width, we would not
expect ion neoclassical effects to contribute to the plasma response in the inner region (because the trapped
ions would average over the spatial structure of the inner region). According to Table 2.4, the
electron banana width is of order a few tenths of a centimeter in a tokamak fusion reactor. Hence, we would not expect electron neoclassical
effects to contribute to the plasma response in very thin
resistive layers. When our neoclassical fluid equations are stripped of specifically neoclassical terms, we shall
refer to then as drift-MHD fluid equations. The “drift” appellation merely indicates that we are still taking diamagnetic flows into account, which necessarily entails treating the ion and electron flows separately.
A second simplifying approximation that we can make is to assume that the perturbed electron temperature and ion temperature profiles are functions of the perturbed electron number density profile, which reduces the number of independent equations that we have to deal with. (See Section 4.2.)
A final simplification is associated with the fact that a tearing mode is a modified shear-Alfvén wave [8], and has very little connection with a compressible-Alfvén wave [8]. For instance, the resonance condition,
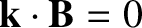 , which determines the position of the rational
surface, is identical to the resonance condition for a shear-Alfvén wave, but differs substantially from that of a compressible-Alfvén wave [2]. Hence, one very effective way of simplifying the resonant layer equations is to remove the irrelevant
physics of compressible-Alfvén waves from them altogether, in the process converting a
drift-MHD response model
into a so-called reduced drift-MHD response model [7,9,10]. The aim of
this chapter is to describe the reduction process, and to derive the reduced drift-MHD fluid equations that will subsequently be used to model the resonant
response of the plasma.
, which determines the position of the rational
surface, is identical to the resonance condition for a shear-Alfvén wave, but differs substantially from that of a compressible-Alfvén wave [2]. Hence, one very effective way of simplifying the resonant layer equations is to remove the irrelevant
physics of compressible-Alfvén waves from them altogether, in the process converting a
drift-MHD response model
into a so-called reduced drift-MHD response model [7,9,10]. The aim of
this chapter is to describe the reduction process, and to derive the reduced drift-MHD fluid equations that will subsequently be used to model the resonant
response of the plasma.