Next: Need for Higher-Order Solution Up: Nonlinear Resonant Response Model Previous: Flux-Surface Average Operator Contents
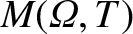 and
and
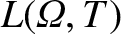 are directly related to the lowest-order perpendicular
velocities of the various plasma species in the island rest frame. In fact, as is clear from Sections 4.2, 5.2, and 8.2,
where
Here,
are directly related to the lowest-order perpendicular
velocities of the various plasma species in the island rest frame. In fact, as is clear from Sections 4.2, 5.2, and 8.2,
where
Here,
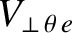 ,
,
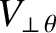 , and
, and
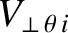 refer to the
refer to the 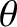 components of the perpendicular electron, MHD, and ion
fluid velocities, respectively. Note that
components of the perpendicular electron, MHD, and ion
fluid velocities, respectively. Note that 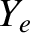 ,
,  , and
, and 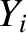 are all zero inside the magnetic separatrix of the island chain.
are all zero inside the magnetic separatrix of the island chain.