Need for Higher-Order Solution

To lowest order in our expansion scheme, the rescaled, reduced, drift-MHD equations, (8.16)–(8.20), require the plasma pressure to be a magnetic flux-surface function. This should come as no surprise. In essence, a magnetic island chain is a helical magnetic equilibrium that evolves (in its local rest frame) on the very slow resistive timescale [8]. Hence, we would expect all of the results derived in Section 2.25 to apply to the plasma in the immediate region of the island chain. 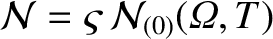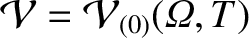Note, however, that, while solving the rescaled, reduced, drift-MHD equations to lowest order tells us that ${\cal N}=\varsigma\,{\cal N}_{(0)}({\mit\Omega},T)$, ${\mit\Phi} =\varsigma\,{\mit\Psi}_{(0)}({\mit\Omega},T)$, and ${\cal V} = {\cal V}_{(0)}({\mit\Omega},T)$, and that the lowest-order current density profile has the form (8.71), the lowest-order solution leaves the flux-surface functions 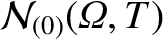${\cal N}_{(0)}({\mit\Omega},T)$, ${\mit\Phi}_{(0)}({\mit\Omega},T)$, ${\cal V}_{(0)}({\mit\Omega},T)$, and $\overline{\cal J}_0({\mit\Omega},T)$ 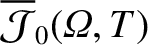completely undetermined. In fact, in order to determine the forms of these four functions, it is necessary to solve the rescaled, reduced, drift-MHD equations to higher order in our expansion scheme. In particular, we need to incorporate the terms that describe the perpendicular diffusion of magnetic flux, ion momentum, and energy into our analysis [5]. The essential point is that the magnetic island chain persists in the plasma for a sufficiently long time that the relatively small perpendicular diffusion terms are able to relax the lowest-order profiles across the island region (and, in fact, across the whole plasma).