Next: Rutherford Island Width Evolution Up: Nonlinear Tearing Mode Stability Previous: Nonlinear Tearing Mode Stability Contents
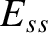 (see Section 3.8), is positive, and is stable
otherwise. In the linear regime, an unstable tearing mode grows exponentially in time on a timescale that
is intermediate between the short hydromagnetic time,
(see Section 3.8), is positive, and is stable
otherwise. In the linear regime, an unstable tearing mode grows exponentially in time on a timescale that
is intermediate between the short hydromagnetic time, 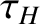 [see Equation (5.43)],
and the much longer resistive diffusion time,
[see Equation (5.43)],
and the much longer resistive diffusion time,  [see Equation (5.49)].
The mode reconnects magnetic flux at the so-called rational surface to produce a helical magnetic island chain. (See Section 5.16.)
The rational surface is the magnetic flux-surface at which the tearing mode resonates with the equilibrium magnetic
field (i.e., at which
[see Equation (5.49)].
The mode reconnects magnetic flux at the so-called rational surface to produce a helical magnetic island chain. (See Section 5.16.)
The rational surface is the magnetic flux-surface at which the tearing mode resonates with the equilibrium magnetic
field (i.e., at which
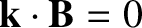 , where
, where 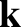 is the wavevector of the mode, and
is the wavevector of the mode, and 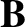 the equilibrium magnetic field).
The
tearing mode also rotates in the laboratory frame at the angular frequency
the equilibrium magnetic field).
The
tearing mode also rotates in the laboratory frame at the angular frequency
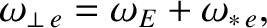 |
(9.1) |
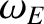 and
and
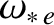 are the E-cross-B and electron diamagnetic frequencies, respectively, at the
rational surface.
[See Equations (5.21), (5.29), (5.44), and (5.45).]
In fact, the previous equation implies that the tearing mode co-rotates with the electron fluid at the rational surface.
are the E-cross-B and electron diamagnetic frequencies, respectively, at the
rational surface.
[See Equations (5.21), (5.29), (5.44), and (5.45).]
In fact, the previous equation implies that the tearing mode co-rotates with the electron fluid at the rational surface.
We saw in Section 5.16 that linear tearing mode theory breaks down as soon as the radial width of the magnetic island chain exceeds the linear layer width, and must be replaced by nonlinear theory. The aim of this chapter is to employ the analysis of Chapter 8 to determine the nonlinear time evolution of an unstable tearing mode.