Next: Resonant Layer Response Up: Error-Field Penetration in Tokamak Previous: Introduction Contents
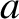 , and simulated major radius
, and simulated major radius  . In accordance with the analysis of Chapter 3, suppose that
the plasma is surrounded by a concentric, radially-thin, rigid, resistive wall of minor radius
. In accordance with the analysis of Chapter 3, suppose that
the plasma is surrounded by a concentric, radially-thin, rigid, resistive wall of minor radius 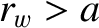 . Likewise,
suppose that the wall is surrounded by a concentric, radially-thin, magnetic field-coil, of minor radius
. Likewise,
suppose that the wall is surrounded by a concentric, radially-thin, magnetic field-coil, of minor radius 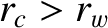 , that carries a non-rotating (in the laboratory frame) helical
current of amplitude
, that carries a non-rotating (in the laboratory frame) helical
current of amplitude 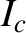 . Let the current possess
. Let the current possess  periods in the poloidal direction, and
periods in the poloidal direction, and 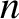 periods in the toroidal direction. The static magnetic
field generated by the field-coil constitutes our error-field. The error-field resonates with the
plasma at the rational magnetic flux-surface, minor radius
periods in the toroidal direction. The static magnetic
field generated by the field-coil constitutes our error-field. The error-field resonates with the
plasma at the rational magnetic flux-surface, minor radius 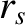 , at which the safety-factor
(see Section 3.2) takes the value
, at which the safety-factor
(see Section 3.2) takes the value 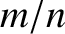 .
.
Setting  (because the error-field is static) in Equations (3.187) and (3.188),
we obtain
(because the error-field is static) in Equations (3.187) and (3.188),
we obtain
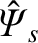 |
![$\displaystyle = -{\rm i}\,\frac{r_s}{R_0\,B_z}\left[\frac{\delta B_r}{m}\right]_{r_s},$](img2488.png) |
(7.2) |
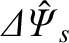 |
![$\displaystyle = -\frac{r_s}{R_0\,B_z}\,[\delta B_\theta]_{r_{s-}}^{r_{s+}},$](img2490.png) |
(7.3) |
 ,
,  ,
, 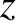 are conventional cylindrical coordinates,
are conventional cylindrical coordinates,
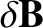 the perturbed magnetic field, and
the perturbed magnetic field, and 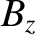 the equilibrium toroidal magnetic field-strength.
(See Sections 3.3, 3.8, and 3.15.)
Clearly,
the equilibrium toroidal magnetic field-strength.
(See Sections 3.3, 3.8, and 3.15.)
Clearly,
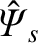 is a measure of the reconnected magnetic flux driven at the rational surface by the error-field, whereas
is a measure of the reconnected magnetic flux driven at the rational surface by the error-field, whereas
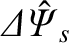 is a measure of the helical current sheet that is induced at the surface. Moreover,
is the (real dimensionless) tearing stability index (of a tearing mode with poloidal mode number
is a measure of the helical current sheet that is induced at the surface. Moreover,
is the (real dimensionless) tearing stability index (of a tearing mode with poloidal mode number  , and
toroidal mode number
, and
toroidal mode number 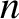 ) in the absence of the wall,
the
(real dimensionless) tearing stability index in the presence of a perfectly conducting wall at
) in the absence of the wall,
the
(real dimensionless) tearing stability index in the presence of a perfectly conducting wall at 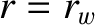 (see Section 3.8), and
(see Section 3.8), and
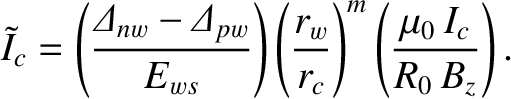 |
(7.6) |
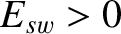 , and the (real dimensionless) wall stability index,
, and the (real dimensionless) wall stability index,
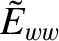 , are defined in Sections 3.9 and 3.17, respectively. We expect
, are defined in Sections 3.9 and 3.17, respectively. We expect
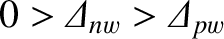 , because the plasma is assumed to be tearing stable (see Chapter 6), and
, because the plasma is assumed to be tearing stable (see Chapter 6), and
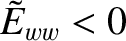 .
In fact, if we make the approximation that the equilibrium plasma current external to the rational magnetic flux-surface is
negligible [i.e.,
.
In fact, if we make the approximation that the equilibrium plasma current external to the rational magnetic flux-surface is
negligible [i.e., 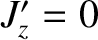 in Equation (3.77)] then it is easily demonstrated that
in Equation (3.77)] then it is easily demonstrated that
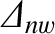 |
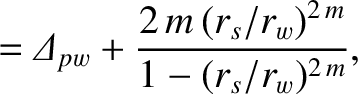 |
(7.7) |
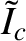 |
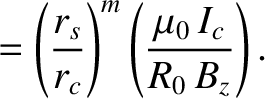 |
(7.8) |
In the radially-thin, resonant layer that surrounds the rational magnetic flux-surface, Equation (5.70) yields
where is the the Lundquist number at the rational surface, and the complex layer matching parameter,
is the the Lundquist number at the rational surface, and the complex layer matching parameter,
 , is defined in
Equation (5.69).
Hence, asymptotic matching between the inner and the outer regions (see Section 4.1) yields
where use has been made of Equations (7.1) and (7.9).
The previous equation specifies the (normalized) reconnected magnetic flux,
, is defined in
Equation (5.69).
Hence, asymptotic matching between the inner and the outer regions (see Section 4.1) yields
where use has been made of Equations (7.1) and (7.9).
The previous equation specifies the (normalized) reconnected magnetic flux,
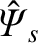 , driven at the rational surface by the (normalized)
error-field coil current,
, driven at the rational surface by the (normalized)
error-field coil current,
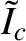 . The complex layer parameter,
. The complex layer parameter,
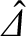 , specifies the strength of a shielding current
that is induced in the resonant layer, and acts to prevent driven magnetic reconnection. Note that the
resistive wall has no influence on
, specifies the strength of a shielding current
that is induced in the resonant layer, and acts to prevent driven magnetic reconnection. Note that the
resistive wall has no influence on
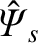 because no eddy currents are induced in the wall by a static
error-field.
because no eddy currents are induced in the wall by a static
error-field.