Next: Bibliography Up: Nonlinear Tearing Mode Stability Previous: Saturated Island Width Contents
 is a magnetic flux-surface label that takes the value zero at the
island O-points, unity on the magnetic separatrix, and is much larger that unity far from the island chain [see Equation (8.55)]. Moreover,
is a magnetic flux-surface label that takes the value zero at the
island O-points, unity on the magnetic separatrix, and is much larger that unity far from the island chain [see Equation (8.55)]. Moreover, 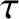 is ratio of the electron and ion pressure gradients at the rational surface
[see Equation (4.5)].
The function
is ratio of the electron and ion pressure gradients at the rational surface
[see Equation (4.5)].
The function
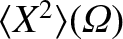 is specified in Section 8.11. Finally, the poloidal components of the perpendicular velocities of the
three fluids in the island rest frame are related to their stream-functions according to Equations (8.72)–(8.74).
is specified in Section 8.11. Finally, the poloidal components of the perpendicular velocities of the
three fluids in the island rest frame are related to their stream-functions according to Equations (8.72)–(8.74).
Figure 9.3 shows typical normalized perpendicular velocity profiles of the electron, MHD, and ion fluids across the O-points and
the X-points of an isolated magnetic island
chain in the island rest frame, as determined from Equations (8.72)–(8.74) and
(9.28)–(9.30) [7]. Here,
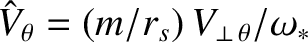 , where
, where  is the poloidal mode number of the tearing mode, and
is the poloidal mode number of the tearing mode, and
 is the diamagnetic frequency at the rational
surface [see Equation (5.47)]. It can be seen that all three fluids co-rotate with the island
chain inside the magnetic separatrix. The ion fluid velocity profile is completely unaffected by the presence of the chain.
On the other hand, the electron and the MHD fluid velocity profiles are modified by the island chain. In particular, both profiles
are discontinuous across the magnetic separatrix. As was explained in Section 8.9, these discontinuities are resolved in a thin layer of
thickness
is the diamagnetic frequency at the rational
surface [see Equation (5.47)]. It can be seen that all three fluids co-rotate with the island
chain inside the magnetic separatrix. The ion fluid velocity profile is completely unaffected by the presence of the chain.
On the other hand, the electron and the MHD fluid velocity profiles are modified by the island chain. In particular, both profiles
are discontinuous across the magnetic separatrix. As was explained in Section 8.9, these discontinuities are resolved in a thin layer of
thickness 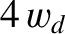 on the separatrix [see Equation (8.84) and Table 8.1]. It is clear from the figure that the island chain rotates in the ion diamagnetic (i.e., negative) direction with respect to
the unperturbed E-cross-B frame at the rational surface [7].
on the separatrix [see Equation (8.84) and Table 8.1]. It is clear from the figure that the island chain rotates in the ion diamagnetic (i.e., negative) direction with respect to
the unperturbed E-cross-B frame at the rational surface [7].
Equations (8.45), (8.63), (9.27), and (9.29) yield
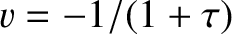 , or
, or
 |
(9.33) |
Finally, it is reasonable to suppose that the critical island width that must be exceeded before a magnetic island chain switches from rotating in the electron direction, with respect to the unperturbed local E-cross-B frame, to rotating in the ion direction is that above which the pressure profile flattens within the separatrix [14].