Next: Zeroth-Order Solution Up: Nonlinear Neoclassical Resonant Response Previous: Rescaled Reduced Neoclassical Drift-MHD Contents
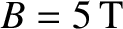 (low-field) or
(low-field) or
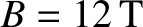 (high-field),
(high-field),
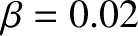 ,
,
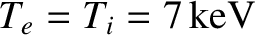 ,
,
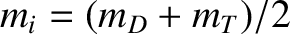 (where
(where 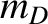 and
and 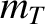 are the deuteron and triton masses, respectively),
are the deuteron and triton masses, respectively),
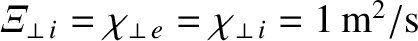 ,
, 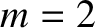 ,
, 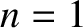 ,
, 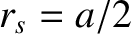 (where
(where 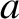 is the minor radius of the plasma),
is the minor radius of the plasma), 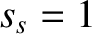 ,
, 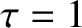 ,
, 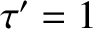 ,
,
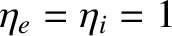 , and
, and
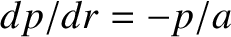 .
.
Let us adopt the orderings
where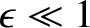 . As is clear from Tables 5.1 and 11.1, these orderings are reasonable provided that the radial width of the
magnetic island chain that develops in the inner region exceeds a few centimeters.
. As is clear from Tables 5.1 and 11.1, these orderings are reasonable provided that the radial width of the
magnetic island chain that develops in the inner region exceeds a few centimeters.
Let us also adopt the orderings
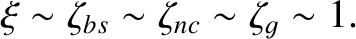 |
(11.93) |
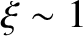 is consistent with the orderings (11.92). Unfortunately, the
orderings
is consistent with the orderings (11.92). Unfortunately, the
orderings
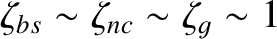 are not consistent with the orderings (11.92). (It would actually be more consistent to
adopt the orderings
are not consistent with the orderings (11.92). (It would actually be more consistent to
adopt the orderings
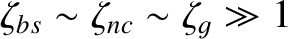 .) Nevertheless, we are forced to adopt the orderings
.) Nevertheless, we are forced to adopt the orderings
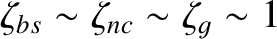 in order to make further progress. (By adopting
these ordering we are essentially ensuring that the bootstrap current and curvature terms in our analysis are not so large that they lead to a breakdown of the
constant-
in order to make further progress. (By adopting
these ordering we are essentially ensuring that the bootstrap current and curvature terms in our analysis are not so large that they lead to a breakdown of the
constant-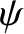 approximation.)
approximation.)
Finally, suppose that
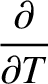 |
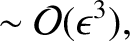 |
(11.94) |
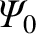 ,
,
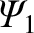 , et cetera are assumed to be
, et cetera are assumed to be
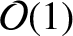 in the inner region.
in the inner region.