Next: Higher-Order Solution Up: Nonlinear Neoclassical Resonant Response Previous: Ordering Scheme Contents
 , Equation (11.72) yields
, Equation (11.72) yields
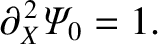 |
(11.100) |
 structure pictured in Figure 5.7. The island O-points correspond to
structure pictured in Figure 5.7. The island O-points correspond to
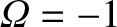 and
and
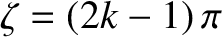 (where
(where  is an integer), the
X-points correspond to
is an integer), the
X-points correspond to
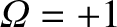 and
and
 , and the magnetic separatrix corresponds to
, and the magnetic separatrix corresponds to
 .
.
To zeroth order in  , Equation (11.71) yields
, Equation (11.71) yields
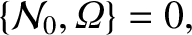 |
(11.102) |
 is an odd function of
is an odd function of  , it
follows that
By symmetry,
, it
follows that
By symmetry,
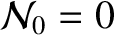 inside the magnetic separatrix of the island chain.
Let
Note that
inside the magnetic separatrix of the island chain.
Let
Note that
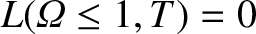 . Equations (11.84) and (11.101) imply that
. Equations (11.84) and (11.101) imply that
To zeroth order in  , Equation (11.68) yields
, Equation (11.68) yields
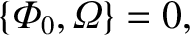 |
(11.106) |
 is an odd function of
is an odd function of 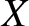 , it follows that
By symmetry,
, it follows that
By symmetry,
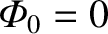 inside the magnetic separatrix of the island chain. Let
Note that
inside the magnetic separatrix of the island chain. Let
Note that
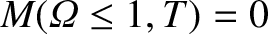 . Equations (11.85) and (11.101) imply that
. Equations (11.85) and (11.101) imply that
To zeroth order in  , Equation (11.69) yields
, Equation (11.69) yields
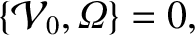 |
(11.110) |
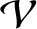 is an even function of
is an even function of 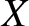 , we can write
, we can write
Finally, to zeroth order in  , Equation (11.70) gives
, Equation (11.70) gives
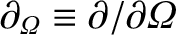 . Note that
. Note that
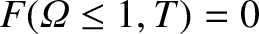 .
.
Let us write
where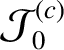 has the symmetry of
has the symmetry of 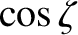 , whereas
, whereas
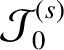 has the symmetry of
has the symmetry of
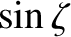 .
It follows from Equations (11.112) and (11.114) that
.
It follows from Equations (11.112) and (11.114) that
![$\displaystyle \{{\cal J}_0^{(c)},{\mit\Omega}\} =-\zeta_g\,\{L\,\vert X\vert,{\...
...Omega}\!\left[M\left(M+\frac{L}{1+\tau}\right)\right]X^2, {\mit\Omega}\right\},$](img3555.png) |
(11.115) |
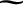 operator is defined in Section 8.6, and
operator is defined in Section 8.6, and
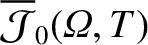 is an undetermined flux-surface function.
is an undetermined flux-surface function.
Equations (11.112) and (11.114) also yield
The flux-surface average (see Section 8.6) of the previous equation gives |
(11.118) |
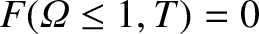 , the previous equation reduces to
, the previous equation reduces to
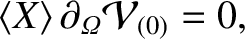 |
(11.119) |
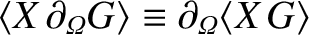 .
Thus, we conclude that
inside the separatrix, and
outside the separatrix. Here, use has been made of
.
Thus, we conclude that
inside the separatrix, and
outside the separatrix. Here, use has been made of
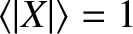 outside the separatrix.
However, the boundary condition (11.86), combined with Equations (11.101), (11.105), (11.109), and (11.113), implies that
outside the separatrix.
However, the boundary condition (11.86), combined with Equations (11.101), (11.105), (11.109), and (11.113), implies that
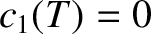 . Finally, Equations (11.117), (11.121), and (11.122) yield
. Finally, Equations (11.117), (11.121), and (11.122) yield