Next: Island Rotation Frequency Up: Neoclassical Tearing Modes Previous: Introduction Contents
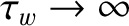 , where
, where 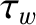 is the time constant of the wall—see Section 3.10), and that there is no current
flowing through the external magnetic field-coil [i.e.,
is the time constant of the wall—see Section 3.10), and that there is no current
flowing through the external magnetic field-coil [i.e.,
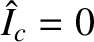 , where
, where 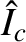 is the normalized coil current—see Equation (3.194)]. In this situation, the magnetic
island chain that develops at the rational surface is said to be isolated (because it is not subject to any outside influence).
For an isolated island chain, Equations (3.187),
(3.188), (7.5), as well as the analysis of Section 9.4, lead to the relation
where
is the normalized coil current—see Equation (3.194)]. In this situation, the magnetic
island chain that develops at the rational surface is said to be isolated (because it is not subject to any outside influence).
For an isolated island chain, Equations (3.187),
(3.188), (7.5), as well as the analysis of Section 9.4, lead to the relation
where
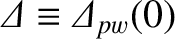 is the (real dimensionless) perfect-wall tearing stability index evaluated at zero island width,
is the (real dimensionless) perfect-wall tearing stability index evaluated at zero island width,
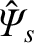 the normalized reconnected helical magnetic flux at the rational surface [see Equation (3.184)],
the normalized reconnected helical magnetic flux at the rational surface [see Equation (3.184)],
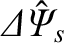 the normalized helical sheet current density at the rational surface [see Equation (3.183)],
the normalized helical sheet current density at the rational surface [see Equation (3.183)], 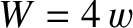 the full radial width of the magnetic
island chain, and
Here,
the full radial width of the magnetic
island chain, and
Here, 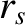 is the minor radius of the rational surface, and the dimensionless parameters
is the minor radius of the rational surface, and the dimensionless parameters 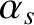 and
and  are defined in Equations (9.16) and (9.17), respectively.
It is clear from the previous equation that
which implies that zero electromagnetic torque is exerted at the rational surface. (See Section 3.13.)
are defined in Equations (9.16) and (9.17), respectively.
It is clear from the previous equation that
which implies that zero electromagnetic torque is exerted at the rational surface. (See Section 3.13.)