Next: Isolated Magnetic Island Chain Up: Neoclassical Tearing Modes Previous: Neoclassical Tearing Modes Contents
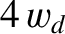 [see Equation (8.84) and Table 8.1] then the plasma pressure profile
is flattened in the region lying within the chain's magnetic separatrix [7].
The flattening of the pressure profile causes a reduction in the bootstrap current [1] inside the separatrix that has a destabilizing
effect on the chain [3]. A tearing mode that is driven unstable by this mechanism, rather than the usual free energy sources for a tearing mode (i.e., global current
and pressure gradients), is known as a neoclassical tearing mode [21].
[see Equation (8.84) and Table 8.1] then the plasma pressure profile
is flattened in the region lying within the chain's magnetic separatrix [7].
The flattening of the pressure profile causes a reduction in the bootstrap current [1] inside the separatrix that has a destabilizing
effect on the chain [3]. A tearing mode that is driven unstable by this mechanism, rather than the usual free energy sources for a tearing mode (i.e., global current
and pressure gradients), is known as a neoclassical tearing mode [21].
Neoclassical tearing modes were originally identified experimentally on the TFTR tokamak [5], and have subsequently been observed in many other tokamaks [12,15,18,23,40]. The flattening of the pressure profile within the
magnetic separatrix of a neoclassical tearing mode leads to a degradation of the energy confinement properties of the plasma [4] that limits the maximum attainable
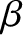 value [see Equation (1.23)] [23].
Consequently, neoclassical tearing modes are nowadays regarded as the main obstacle to obtaining
value [see Equation (1.23)] [23].
Consequently, neoclassical tearing modes are nowadays regarded as the main obstacle to obtaining
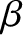 values in tokamak plasmas that are adequate for the achievement of
thermonuclear fusion [2,21,32].
values in tokamak plasmas that are adequate for the achievement of
thermonuclear fusion [2,21,32].
The fact that a magnetic island chain can only locally flatten
the plasma pressure profile (and, thereby, generate a destabilizing local reduction in the bootstrap current) when its radial width exceeds the critical value 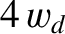 leads to the conclusion that neoclassical tearing modes are actually meta-stable [7].
In other words, some sort of seed perturbation must be applied to the relevant rational magnetic flux-surface in order to trigger a neoclassical tearing mode.
In practice, the seed perturbation usually takes the form of a transient magnetic perturbation that is resonant at the
rational surface [16]. Such perturbations arise naturally in tokamak plasmas as a consequence of plasma instabilities such as internal kink modes and edge localized modes [36].
leads to the conclusion that neoclassical tearing modes are actually meta-stable [7].
In other words, some sort of seed perturbation must be applied to the relevant rational magnetic flux-surface in order to trigger a neoclassical tearing mode.
In practice, the seed perturbation usually takes the form of a transient magnetic perturbation that is resonant at the
rational surface [16]. Such perturbations arise naturally in tokamak plasmas as a consequence of plasma instabilities such as internal kink modes and edge localized modes [36].
Neoclassical tearing modes can be stabilized by driving a parallel (to the magnetic field) current in the vicinity of the rational surface by means of radio frequency electromagnetic waves injected into the plasma; the idea is to replace the missing bootstrap current within the island chain's magnetic separatrix [15,22,25,29,38,39].
The aim of this chapter is to use the nonlinear neoclassical resonant response model derived in the previous chapter to investigate the physics of neoclassical tearing modes.