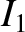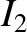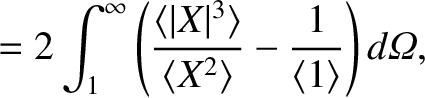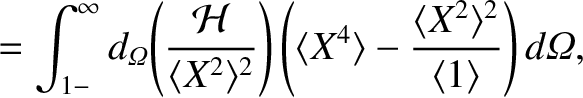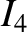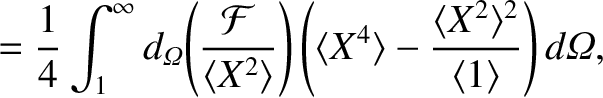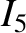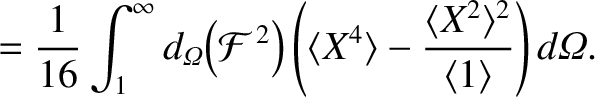The asymptotic matching relations (11.90) and (11.91) can
be re-expressed in the forms (see Section 8.10),
Equations (11.123), (11.136), and (11.141) yield
![$\displaystyle {\rm Im}\!\left(\frac{{\mit\Delta}\hat{\mit\Psi}_s}{\hat{\mit\Psi...
...e X^{\,2}\rangle-\vert X\vert\right){\cal F}\right]\right\rangle d{\mit\Omega}.$](img3596.png) |
(11.142) |
Employing the easily proved identity
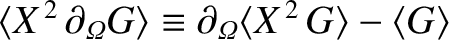 ,
we obtain
where use has been made of Equations (11.138), (11.139), as well as the fact that
,
we obtain
where use has been made of Equations (11.138), (11.139), as well as the fact that
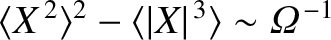 as
as
 .
However, according to Equation (11.137),
where use has been made of Equations (11.138) and (11.139).
The previous equation yields
.
However, according to Equation (11.137),
where use has been made of Equations (11.138) and (11.139).
The previous equation yields
![$\displaystyle \left[r\,\frac{d\omega_E}{dr}\right]_{r_{s-}}^{r_{s+}}=\left(\fra...
...)
{\rm Im}\!\left(\frac{{\mit\Delta}\hat{\mit\Psi}_s}{\hat{\mit\Psi}_s}\right),$](img3602.png) |
(11.145) |
where use has been made of Equations (8.23), (8.25), (8.27), and (8.46), and (8.103).
Here, 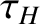 is the hydromagnetic time [see Equation (5.43)], and
is the hydromagnetic time [see Equation (5.43)], and
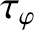 is the toroidal momentum confinement time [see Equation (5.50)].
Equation (11.145) can also be obtained by integrating Equation (3.165) across the rational surface, making use of Equation (3.140), as well as the
identification
is the toroidal momentum confinement time [see Equation (5.50)].
Equation (11.145) can also be obtained by integrating Equation (3.165) across the rational surface, making use of Equation (3.140), as well as the
identification
![$\displaystyle \left[r\,\frac{d\omega_E}{dr}\right]_{r_{s-}}^{r_{s+}} = -n\left[r\,\frac{\partial{\mit\Delta\Omega}_z}{\partial r}\right]_{r_{s-}}^{r_{s+}}.$](img3603.png) |
(11.146) |
If we compare Equation (11.145) with Equation (8.102) then we can see that the discontinuity in the MHD fluid
velocity gradient that develops at the rational
surface is a factor
 smaller in our neoclassical drift-MHD model than the corresponding discontinuity in our non-neoclassical drift-MHD model.
The reason for this reduction is that the strong poloidal flow-damping present in the former model prevents the poloidal plasma rotation profile from
being modified by the localized electromagnetic torque produced at the rational surface. Instead, only the toroidal plasma rotation profile is modified by the
electromagnetic torque [4,18].
smaller in our neoclassical drift-MHD model than the corresponding discontinuity in our non-neoclassical drift-MHD model.
The reason for this reduction is that the strong poloidal flow-damping present in the former model prevents the poloidal plasma rotation profile from
being modified by the localized electromagnetic torque produced at the rational surface. Instead, only the toroidal plasma rotation profile is modified by the
electromagnetic torque [4,18].
It follows from Equations (11.113), (11.127), (11.130), (11.136), and (11.140) that
Here,
![\begin{displaymath}{\cal H}({\mit\Omega})=\left\{
\begin{array}{llr}
0&&-1\leq {...
...\Omega}\leq 1\\ [0.5ex]
1&~~&{\mit\Omega}>1
\end{array}\right.,\end{displaymath}](img3610.png) |
(11.148) |
and use has been made of the fact that
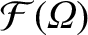 is continuous across the separatrix.
The previous equation can be combined with Equations (8.10), (8.23)–(8.27), (8.103), and (11.77), (11.79), and (11.144) to
give [2,3,7,14,15,20,21,23]
where
is continuous across the separatrix.
The previous equation can be combined with Equations (8.10), (8.23)–(8.27), (8.103), and (11.77), (11.79), and (11.144) to
give [2,3,7,14,15,20,21,23]
where
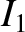 |
 |
(11.150) |
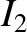 |
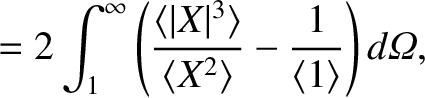 |
(11.151) |
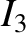 |
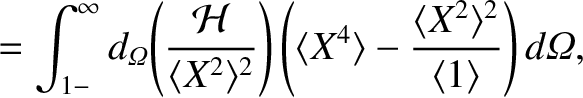 |
(11.152) |
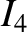 |
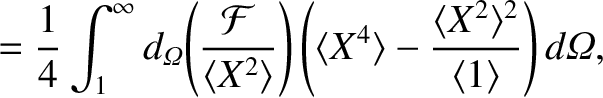 |
(11.153) |
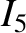 |
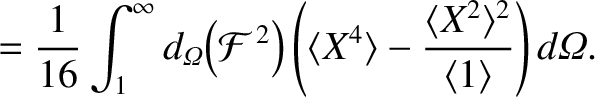 |
(11.154) |
![$\displaystyle {\rm Im}\!\left(\frac{{\mit\Delta}\hat{\mit\Psi}_s}{\hat{\mit\Psi...
...e X^{\,2}\rangle-\vert X\vert\right){\cal F}\right]\right\rangle d{\mit\Omega}.$](img3596.png)
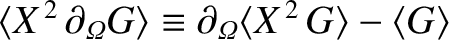 ,
we obtain
,
we obtain
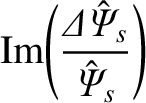
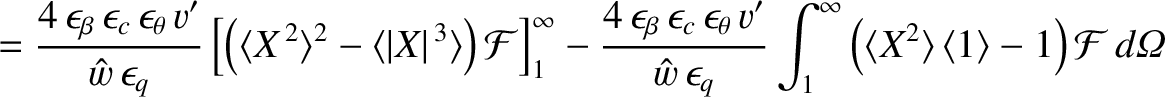

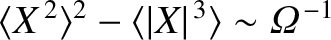 as
as
 .
However, according to Equation (11.137),
where use has been made of Equations (11.138) and (11.139).
The previous equation yields
where use has been made of Equations (8.23), (8.25), (8.27), and (8.46), and (8.103).
Here,
.
However, according to Equation (11.137),
where use has been made of Equations (11.138) and (11.139).
The previous equation yields
where use has been made of Equations (8.23), (8.25), (8.27), and (8.46), and (8.103).
Here, 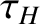 is the hydromagnetic time [see Equation (5.43)], and
is the hydromagnetic time [see Equation (5.43)], and
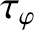 is the toroidal momentum confinement time [see Equation (5.50)].
Equation (11.145) can also be obtained by integrating Equation (3.165) across the rational surface, making use of Equation (3.140), as well as the
identification
is the toroidal momentum confinement time [see Equation (5.50)].
Equation (11.145) can also be obtained by integrating Equation (3.165) across the rational surface, making use of Equation (3.140), as well as the
identification
![$\displaystyle \left[r\,\frac{d\omega_E}{dr}\right]_{r_{s-}}^{r_{s+}} = -n\left[r\,\frac{\partial{\mit\Delta\Omega}_z}{\partial r}\right]_{r_{s-}}^{r_{s+}}.$](img3603.png)
 smaller in our neoclassical drift-MHD model than the corresponding discontinuity in our non-neoclassical drift-MHD model.
The reason for this reduction is that the strong poloidal flow-damping present in the former model prevents the poloidal plasma rotation profile from
being modified by the localized electromagnetic torque produced at the rational surface. Instead, only the toroidal plasma rotation profile is modified by the
electromagnetic torque [4,18].
smaller in our neoclassical drift-MHD model than the corresponding discontinuity in our non-neoclassical drift-MHD model.
The reason for this reduction is that the strong poloidal flow-damping present in the former model prevents the poloidal plasma rotation profile from
being modified by the localized electromagnetic torque produced at the rational surface. Instead, only the toroidal plasma rotation profile is modified by the
electromagnetic torque [4,18].
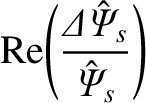
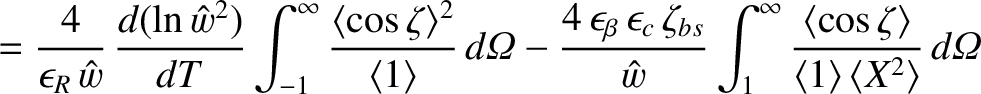
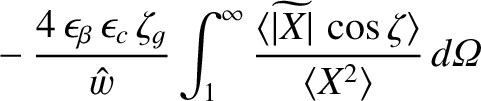
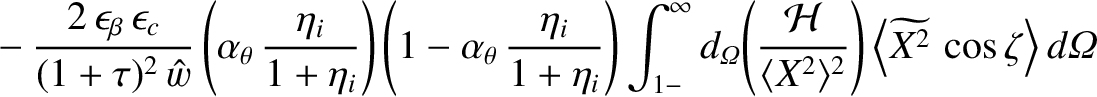
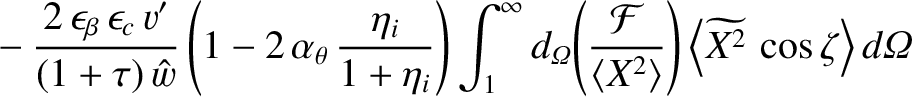

![\begin{displaymath}{\cal H}({\mit\Omega})=\left\{
\begin{array}{llr}
0&&-1\leq {...
...\Omega}\leq 1\\ [0.5ex]
1&~~&{\mit\Omega}>1
\end{array}\right.,\end{displaymath}](img3610.png)
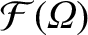 is continuous across the separatrix.
The previous equation can be combined with Equations (8.10), (8.23)–(8.27), (8.103), and (11.77), (11.79), and (11.144) to
give [2,3,7,14,15,20,21,23]
where
is continuous across the separatrix.
The previous equation can be combined with Equations (8.10), (8.23)–(8.27), (8.103), and (11.77), (11.79), and (11.144) to
give [2,3,7,14,15,20,21,23]
where