Next: Bibliography Up: Nonlinear Neoclassical Resonant Response Previous: Asymptotic Matching Contents
It is helpful to define the new magnetic flux-surface label
![$k=[(1+{\mit\Omega})/2]^{1/2}$](img2907.png) . (See Section 8.11.)
It follows from Equation (11.101) that
. (See Section 8.11.)
It follows from Equation (11.101) that 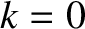 at the O-points of the magnetic island chain, and
at the O-points of the magnetic island chain, and 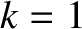 on the magnetic separatrix.
Hence, we can write
on the magnetic separatrix.
Hence, we can write
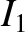 |
![$\displaystyle = \int_0^\infty \frac{4\,[(2\,k^2-1)\,{\cal A}-2\,k^2\,{\cal C}]^{2}}{{\cal A}}\,dk,$](img3625.png) |
(11.155) |
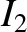 |
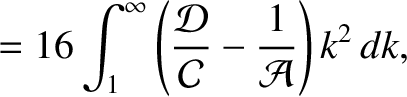 |
(11.156) |
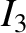 |
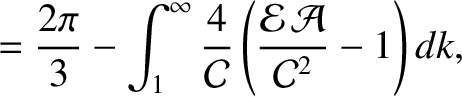 |
(11.157) |
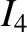 |
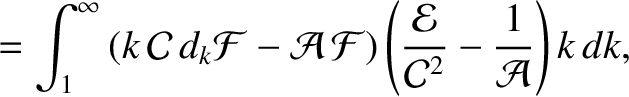 |
(11.158) |
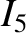 |
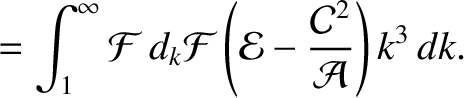 |
(11.159) |
![$\displaystyle d_k\!\left[{\cal C}\,d_k(k\,{\cal C}\,{\cal F})\right] = \lambda_{\theta\varphi}\,({\cal A}\,{\cal C}-1)\,k\,{\cal F},$](img3630.png) |
(11.160) |
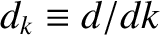 , and
, and
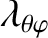 |
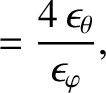 |
(11.161) |
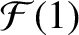 |
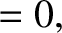 |
(11.162) |
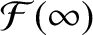 |
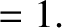 |
(11.163) |
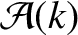 ,
,
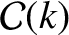 ,
,
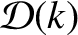 , and
, and
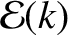 are defined in Section 8.11.
Note that the factor
are defined in Section 8.11.
Note that the factor  in Equation (11.157) is generated by the discontinuity in the function
in Equation (11.157) is generated by the discontinuity in the function
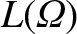 (i.e., the discontinuity in the pressure gradient) across the
separatrix of the magnetic island chain [23]. If this contribution is omitted then the sign of the integral
(i.e., the discontinuity in the pressure gradient) across the
separatrix of the magnetic island chain [23]. If this contribution is omitted then the sign of the integral 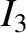 is reversed.
is reversed.
The values of the first three integrals are
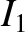 |
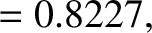 |
(11.164) |
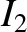 |
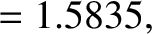 |
(11.165) |
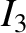 |
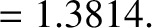 |
(11.166) |
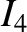 and
and 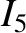 as functions of
as functions of
 .
Note that
.
Note that 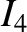 and
and 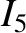 are both only very weak functions of
are both only very weak functions of
 .
.