Next: Island Phase Evolution Equations Up: Mode Locking in Tokamak Previous: Asymptotic Matching Contents
 ,
, 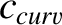 , and
, and 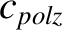 are defined in Equations (12.16), (12.17), and (12.18), respectively, whereas
are defined in Equations (12.16), (12.17), and (12.18), respectively, whereas
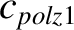 |
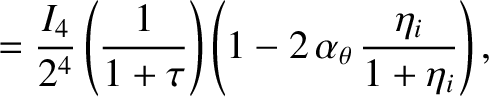 |
(13.5) |
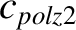 |
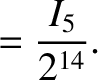 |
(13.6) |
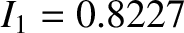 ,
, 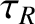 is the resistive diffusion time [see Equation (5.49)],
is the resistive diffusion time [see Equation (5.49)],
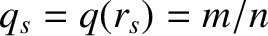 the safety-factor at the rational surface [see Equation (3.2)],
the safety-factor at the rational surface [see Equation (3.2)],
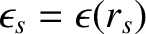 the inverse aspect-ratio at the
rational surface [see Equation (3.18)],
the inverse aspect-ratio at the
rational surface [see Equation (3.18)],
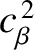 a dimensionless measure of the plasma pressure at the rational surface [see Equations (4.65) and (4.66)],
a dimensionless measure of the plasma pressure at the rational surface [see Equations (4.65) and (4.66)], 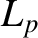 the effective pressure gradient scale-length at the rational surface [see Equation (8.35)],
the effective pressure gradient scale-length at the rational surface [see Equation (8.35)], 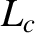 the magnetic curvature length at the rational
surface [see Equation (11.57)],
the magnetic curvature length at the rational
surface [see Equation (11.57)], 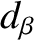 the ion sound radius [see Equation (4.75)],
the ion sound radius [see Equation (4.75)], 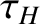 the hydromagnetic time [see Equation (5.43)],
the hydromagnetic time [see Equation (5.43)],
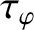 the toroidal momentum confinement time [see Equation (5.50)],
the toroidal momentum confinement time [see Equation (5.50)], 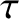 the ratio of the electron and ion pressure gradients at the rational surface
[see Equation (4.5)], and
the ratio of the electron and ion pressure gradients at the rational surface
[see Equation (4.5)], and 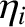 a dimensionless measure of the ion temperature gradient at the rational surface [see Equation (4.3)]. Finally, the dimensionless ion neoclassical poloidal flow-damping parameter
a dimensionless measure of the ion temperature gradient at the rational surface [see Equation (4.3)]. Finally, the dimensionless ion neoclassical poloidal flow-damping parameter
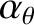 is
defined in Equation (12.6), and the dimensionless integrals
is
defined in Equation (12.6), and the dimensionless integrals 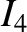 and
and 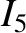 are specified in Figure 11.1. Note that, in writing Equation (13.4), we have assumed that
are specified in Figure 11.1. Note that, in writing Equation (13.4), we have assumed that 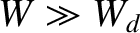 [see Equation (12.20)] (i.e., that the island chain is sufficiently wide that the plasma pressure profile is flattened within its magnetic separatrix).
[see Equation (12.20)] (i.e., that the island chain is sufficiently wide that the plasma pressure profile is flattened within its magnetic separatrix).
The first term on the right-hand side of Equation (13.4) is the linear tearing stability index,
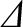 [11].
The second term is a stabilizing (i.e., negative) saturation term [12].
The third term is a destabilizing (i.e., positive) term that is due to the loss of the bootstrap current within the magnetic
separatrix of the island chain consequent on the flattening of the plasma pressure profile in this region [4].
The fourth term is a stabilizing term due to magnetic field-line curvature [13,18].
The fifth term represents the stabilizing effect of the ion polarization
current induced in the vicinity of the rational surface when the ion fluid is diverted around the island chain's magnetic separatrix
[7,25,26,27]. The sixth and seventh terms are additional ion polarization terms that arise from the modified
ion flow in the immediate vicinity of the island chain when the chain is subject to an externally generated electromagnetic torque [10,27].
The final term is due to the direct interaction between the island chain and the resonant magnetic perturbation [9].
[11].
The second term is a stabilizing (i.e., negative) saturation term [12].
The third term is a destabilizing (i.e., positive) term that is due to the loss of the bootstrap current within the magnetic
separatrix of the island chain consequent on the flattening of the plasma pressure profile in this region [4].
The fourth term is a stabilizing term due to magnetic field-line curvature [13,18].
The fifth term represents the stabilizing effect of the ion polarization
current induced in the vicinity of the rational surface when the ion fluid is diverted around the island chain's magnetic separatrix
[7,25,26,27]. The sixth and seventh terms are additional ion polarization terms that arise from the modified
ion flow in the immediate vicinity of the island chain when the chain is subject to an externally generated electromagnetic torque [10,27].
The final term is due to the direct interaction between the island chain and the resonant magnetic perturbation [9].
It is convenient to rewrite Equation (13.4) in the form
Here,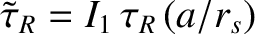 ,
,
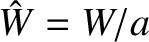 , and
, and
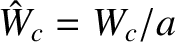 , where
, where 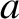 is the plasma minor radius. Moreover,
is the plasma minor radius. Moreover, 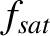 ,
, 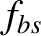 ,
, 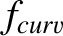 , and
, and
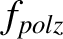 are defined in Equations (12.23)–(12.26), respectively, whereas
are defined in Equations (12.23)–(12.26), respectively, whereas
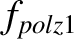 |
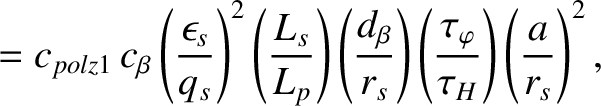 |
(13.8) |
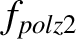 |
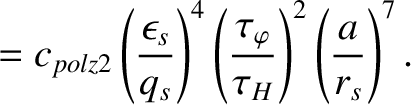 |
(13.9) |
Table 12.1 gives estimates for the various dimensionless parameters that characterize the right-hand side of the generalized Rutherford equation, (13.7), for the case of a
low-field and a high-field tokamak fusion reactor. (See Chapter 1.) These estimates are made using the following assumptions:
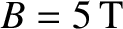 (low-field) or
(low-field) or
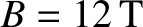 (high-field),
(high-field),
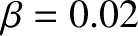 ,
,
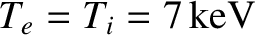 ,
,
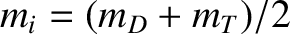 (where
(where 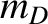 and
and 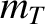 are the deuteron and triton masses, respectively),
are the deuteron and triton masses, respectively),
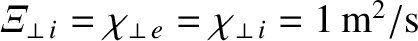 ,
, 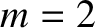 ,
, 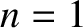 ,
, 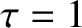 ,
,
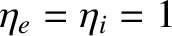 , and
, and
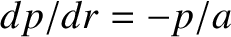 . The plasma equilibrium is
assumed to be of the Wesson type with
. The plasma equilibrium is
assumed to be of the Wesson type with 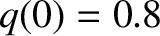 ,
, 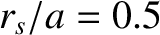 , and
, and
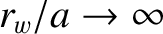 . (See Section 9.4.)
. (See Section 9.4.)