Next: Analytic Solution of Phase Up: Mode Locking in Tokamak Previous: Rutherford Island Width Evolution Contents
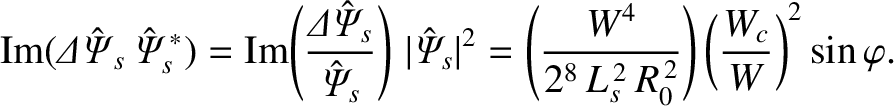 |
(13.10) |
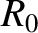 is the major radius of the plasma, and use has been made of Equations (5.129) and (13.1). The previous equation
can be combined with Equations (3.189)–(3.191) and (13.2) to give the following set of equations that govern the time evolution of the
magnetic island chain's helical phase:
Here,
is the major radius of the plasma, and use has been made of Equations (5.129) and (13.1). The previous equation
can be combined with Equations (3.189)–(3.191) and (13.2) to give the following set of equations that govern the time evolution of the
magnetic island chain's helical phase:
Here, 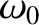 is the natural frequency of the magnetic island chain (i.e., the chain's rotation frequency in the absence of the resonant magnetic
perturbation),
is the natural frequency of the magnetic island chain (i.e., the chain's rotation frequency in the absence of the resonant magnetic
perturbation),
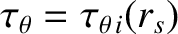 the ion neoclassical poloidal
flow-damping time at the rational surface [see Equation (2.332)], and
the ion neoclassical poloidal
flow-damping time at the rational surface [see Equation (2.332)], and
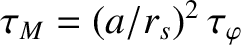 .
Moreover,
.
Moreover, 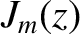 is a Bessel function, and
is a Bessel function, and 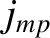 denotes its
denotes its 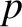 th zero [1]. In deriving the previous equations, use has been
made of Equations (4.23), (5.43), and (5.129).
th zero [1]. In deriving the previous equations, use has been
made of Equations (4.23), (5.43), and (5.129).