Next: Rutherford Island Width Evolution Up: Mode Locking in Tokamak Previous: Introduction Contents
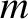 periods in the poloidal direction, and
periods in the poloidal direction, and 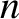 periods in the toroidal direction. Let
periods in the toroidal direction. Let 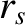 be the minor radius of the rational
surface.
be the minor radius of the rational
surface.
Let us reuse the analysis of Sections 3.17, 7.2, and 9.4. In the absence of a wall (i.e., 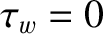 ), but in the presence of a static magnetic perturbation generated by a steady
helical current,
), but in the presence of a static magnetic perturbation generated by a steady
helical current, 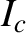 , with
, with 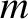 periods in the poloidal direction, and
periods in the poloidal direction, and 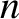 periods in the toroidal direction, running though an external magnetic field-coil located
outside the plasma at minor radius
periods in the toroidal direction, running though an external magnetic field-coil located
outside the plasma at minor radius 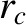 , we find that [9]
, we find that [9]
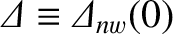 is the (real dimensionless) no-wall tearing stability index evaluated at zero island width [see Equation (7.4)],
is the (real dimensionless) no-wall tearing stability index evaluated at zero island width [see Equation (7.4)],
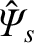 the normalized reconnected helical magnetic flux at the rational surface [see Equation (3.184)],
the normalized reconnected helical magnetic flux at the rational surface [see Equation (3.184)],
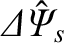 the normalized helical sheet current density at the rational surface [see Equation (3.183)],
the normalized helical sheet current density at the rational surface [see Equation (3.183)], 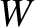 the full radial width of the magnetic
island chain [see Equation (5.129)],
the full radial width of the magnetic
island chain [see Equation (5.129)], 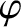 the helical phase of the island chain measured with respect to that of the static resonant magnetic perturbation,
the helical phase of the island chain measured with respect to that of the static resonant magnetic perturbation, 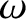 the
instantaneous island rotation frequency in the laboratory frame [see Equation (3.189)],
the
instantaneous island rotation frequency in the laboratory frame [see Equation (3.189)], 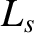 the magnetic shear-length at the rational surface [see Equation (5.27)],
and
the magnetic shear-length at the rational surface [see Equation (5.27)],
and 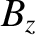 the equilibrium toroidal magnetic field-strength. Moreover,
the equilibrium toroidal magnetic field-strength. Moreover, 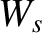 is specified in Equation (12.2), and
is specified in Equation (12.2), and 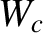 is a measure of the width of the locked magnetic
island chain that the resonant magnetic perturbation would induce at the rational surface in the absence of localized shielding currents. Finally,
we have made the simplifying approximation that the equilibrium plasma current external to the rational surface is negligible. (See Section 7.2.)
is a measure of the width of the locked magnetic
island chain that the resonant magnetic perturbation would induce at the rational surface in the absence of localized shielding currents. Finally,
we have made the simplifying approximation that the equilibrium plasma current external to the rational surface is negligible. (See Section 7.2.)