Table 13.2 gives estimates for the characteristic timescales that govern the time evolution of the width and phase of a magnetic island chain
interacting with a static resonant magnetic perturbation in a low-field and a high-field tokamak fusion reactor. These estimates are made using the same assumptions used to produce the estimates shown in Table 13.1. In addition, the natural frequency of the tearing mode is assumed to be equal to the diamagnetic frequency,
 [see Equation (5.47)]. (See Section 5.15.)
Now, the island phase evolves on the timescale
[see Equation (5.47)]. (See Section 5.15.)
Now, the island phase evolves on the timescale
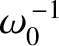 , whereas the island width evolves on the timescale
, whereas the island width evolves on the timescale
 . It can be
seen that the former timescale is very much shorter than the latter. Thus, to a first approximation, it is reasonable to suppose that the island width remains constant as the island
phase evolves. This implies that the island phase evolution equations, (13.11)–(13.14), can be solved independently of the island width evolution equation, (13.7).
. It can be
seen that the former timescale is very much shorter than the latter. Thus, to a first approximation, it is reasonable to suppose that the island width remains constant as the island
phase evolves. This implies that the island phase evolution equations, (13.11)–(13.14), can be solved independently of the island width evolution equation, (13.7).
In this section, we shall solve the island phase evolution equations, (13.11)–(13.14), analytically via an expansion in a dimensionless small parameter,
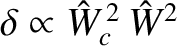 , that is defined in Equation (13.29).
To lowest order, Equations (13.13) and (13.14) yield
, that is defined in Equation (13.29).
To lowest order, Equations (13.13) and (13.14) yield
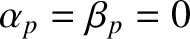 . Hence, Equations (13.11) and (13.12) give
. Hence, Equations (13.11) and (13.12) give
respectively. Of course, this lowest-order solution corresponds to the island chain rotating steadily at its natural frequency.
To first order, Equations (13.13), (13.14), and (13.16) yield
Let us write
It follows that
Equations (13.11), (13.19), and (13.20) give
![$\displaystyle \omega = \omega_0 -{\rm Re}\left[\sum_{p=1,\infty}\left(\hat{\alpha}_{p\,1}+\hat{\beta}_{p\,1}\right){\rm e}^{-{\rm i}\,\omega_0\,t}\right].$](img3860.png) |
(13.23) |
However, according to Equations (13.21) and (13.22),
Now, it can be demonstrated that
![$\displaystyle \sum_{p=1,\infty}\frac{[J_1(j_{1p}\,r_s/a)]^{\,2}}{[J_2(j_{1p})]^...
...c{1}{4}\,\frac{1}{(-{\rm i}\,\omega_0+1/\tau_\theta)^{1/2}\,\tau_\varphi^{1/2}}$](img3865.png) |
(13.26) |
in the limit that
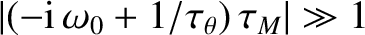 . As is clear from Table 13.2, the previous inequality is easily satisfied in a tokamak fusion reactor. Likewise,
it can be demonstrated that
. As is clear from Table 13.2, the previous inequality is easily satisfied in a tokamak fusion reactor. Likewise,
it can be demonstrated that
![$\displaystyle \sum_{p=1,\infty}\frac{[J_0(j_{0p}\,r_s/a)]^{\,2}}{[J_1(j_{0p})]^...
...}^{\,2})}\simeq \frac{1}{4}\,\frac{1}{(-{\rm i}\,\omega_0\,\tau_\varphi)^{1/2}}$](img3867.png) |
(13.27) |
in the limit that
 . As is apparent from Table 13.2, the previous inequality is also easily satisfied in a tokamak fusion reactor. Thus, we
obtain
. As is apparent from Table 13.2, the previous inequality is also easily satisfied in a tokamak fusion reactor. Thus, we
obtain
![$\displaystyle \omega(t)= \omega_0\left[1+\delta\,C_1\,\cos(\omega_0\,t) -\delta\, S_1\,\sin(\omega_0\,t)\right],$](img3869.png) |
(13.28) |
where
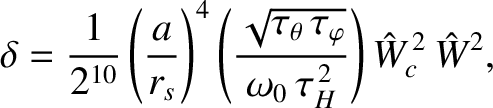 |
(13.29) |
and
According to Equation (13.28), the electromagnetic locking torque exerted by the static magnetic perturbation on the island chain generates a periodic modulation in the
chain's rotation frequency that oscillates at the natural frequency.
Equations (13.12) and (13.28) give
 |
(13.32) |
Finally, we obtain
To second order, Equations (13.13), (13.14), and (13.33) yield
Let us write
If follows that
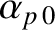 |
![$\displaystyle =\frac{\tau_\varphi}{2^9\,\tau_H^{\,2}}
\left(\frac{a}{r_s}\right...
..._{1p}\,r_s/a)]^{\,2}}{[J_2(j_{1p})]^{\,2}\,(\tau_M/\tau_\theta+ j_{1p}^{\,2})},$](img3889.png) |
(13.39) |
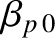 |
![$\displaystyle = \frac{\tau_\varphi}{2^9\,\tau_H^{\,2}}\left(\frac{a}{r_s}\right...
...ta\,S_1\,\frac{[J_0(j_{0p}\,r_s/a)]^{\,2}}{[J_1(j_{0p})]^{\,2}\, j_{0p}^{\,2}},$](img3891.png) |
(13.40) |
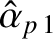 |
![$\displaystyle = \frac{\tau_\varphi}{2^8\,\tau_H^{\,2}}
\left(\frac{a}{r_s}\righ...
...2(j_{1p})]^{\,2}\,[(-{\rm i}\,\omega_0+1/\tau_\theta)\,\tau_M + j_{1p}^{\,2}]},$](img3892.png) |
(13.41) |
 |
![$\displaystyle = \frac{\tau_\varphi}{2^8\,\tau_H^{\,2}}\left(\frac{a}{r_s}\right...
...s/a)]^{\,2}}{[J_1(j_{0p})]^{\,2}\,(-{\rm i}\,\omega_0\,\tau_M + j_{0p}^{\,2})},$](img3893.png) |
(13.42) |
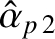 |
![$\displaystyle = \frac{\tau_\varphi}{2^9\,\tau_H^{\,2}}
\left(\frac{a}{r_s}\righ...
..._{1p})]^{\,2}\,[(-{\rm i}\,2\,\omega_0+1/\tau_\theta)\,\tau_M + j_{1p}^{\,2}]},$](img3895.png) |
(13.43) |
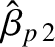 |
![$\displaystyle = \frac{\tau_\varphi}{2^9\,\tau_H^{\,2}}\left(\frac{a}{r_s}\right...
...)]^{\,2}}{[J_1(j_{0p})]^{\,2}\,(-{\rm i}\,2\,\omega_0\,\tau_M + j_{0p}^{\,2})}.$](img3897.png) |
(13.44) |
Let us define the period-average operator:
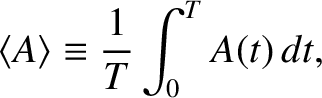 |
(13.49) |
where
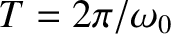 . It is clear from Equation (13.45) that
. It is clear from Equation (13.45) that
![$\displaystyle \langle\omega\rangle = \omega_0\left[1-\frac{1}{2}\,\delta^2\,S_0\,S_1 + {\cal O}(\delta^3)\right].$](img3908.png) |
(13.50) |
In other words, the electromagnetic locking torque exerted by a static resonant magnetic perturbation on the rotating island chain causes an average reduction in the
chain's rotation frequency that is proportional to
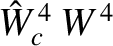 (i.e., to the square of the current flowing in the external magnetic field-coil that generates the perturbation). [See Equations (13.3) and (13.29).]
(i.e., to the square of the current flowing in the external magnetic field-coil that generates the perturbation). [See Equations (13.3) and (13.29).]
Equation (13.33) yields
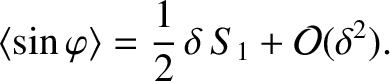 |
(13.51) |
Now, the electromagnetic locking torque exerted on the island chain is proportional to
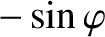 . Furthermore, as the island chain rotates past the static resonant magnetic perturbation, its rotation is alternately
accelerated (when
. Furthermore, as the island chain rotates past the static resonant magnetic perturbation, its rotation is alternately
accelerated (when
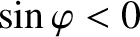 ) and decelerated (when
) and decelerated (when
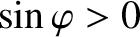 ) by this torque. However, as is apparent from the previous equation, the uneven rotation of the island chain in the presence of the perturbation [see Equation (13.45)]
causes it to spend more time in the helical phase relative to the perturbation in which it is decelerated by the torque than in the phase that it is accelerated [9,14,24,28]. This explains the net
slowing of the chain's rotation indicated in Equation (13.50).
) by this torque. However, as is apparent from the previous equation, the uneven rotation of the island chain in the presence of the perturbation [see Equation (13.45)]
causes it to spend more time in the helical phase relative to the perturbation in which it is decelerated by the torque than in the phase that it is accelerated [9,14,24,28]. This explains the net
slowing of the chain's rotation indicated in Equation (13.50).
Equation (13.34) yields
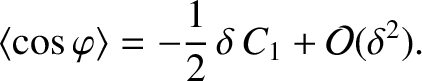 |
(13.52) |
Now, the direct interaction between the static magnetic perturbation and the island chain generates a term in the Rutherford island width
evolution equation that is proportional to
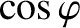 . [See Equation (13.7).] Furthermore, as the island chain rotates past the static resonant magnetic perturbation, this term alternately
destabilizes (when
. [See Equation (13.7).] Furthermore, as the island chain rotates past the static resonant magnetic perturbation, this term alternately
destabilizes (when
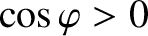 ) and stabilizes (when
) and stabilizes (when
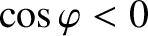 ) the chain. However, as is apparent from the previous equation, the uneven rotation of the island chain in the presence of the perturbation [see Equation (13.45)]
causes it to spend more time in the helical phase relative to the perturbation in which it is stabilized by the interaction term than in the phase that it is destabilized [9,14,24,28]. Thus, there is a net stabilizing effect when a rotating magnetic island chain interacts directly with a static resonant magnetic perturbation.
) the chain. However, as is apparent from the previous equation, the uneven rotation of the island chain in the presence of the perturbation [see Equation (13.45)]
causes it to spend more time in the helical phase relative to the perturbation in which it is stabilized by the interaction term than in the phase that it is destabilized [9,14,24,28]. Thus, there is a net stabilizing effect when a rotating magnetic island chain interacts directly with a static resonant magnetic perturbation.
 [see Equation (5.47)]. (See Section 5.15.)
Now, the island phase evolves on the timescale
[see Equation (5.47)]. (See Section 5.15.)
Now, the island phase evolves on the timescale
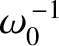 , whereas the island width evolves on the timescale
, whereas the island width evolves on the timescale
 . It can be
seen that the former timescale is very much shorter than the latter. Thus, to a first approximation, it is reasonable to suppose that the island width remains constant as the island
phase evolves. This implies that the island phase evolution equations, (13.11)–(13.14), can be solved independently of the island width evolution equation, (13.7).
. It can be
seen that the former timescale is very much shorter than the latter. Thus, to a first approximation, it is reasonable to suppose that the island width remains constant as the island
phase evolves. This implies that the island phase evolution equations, (13.11)–(13.14), can be solved independently of the island width evolution equation, (13.7).
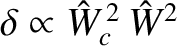 , that is defined in Equation (13.29).
To lowest order, Equations (13.13) and (13.14) yield
, that is defined in Equation (13.29).
To lowest order, Equations (13.13) and (13.14) yield
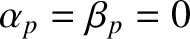 . Hence, Equations (13.11) and (13.12) give
. Hence, Equations (13.11) and (13.12) give
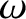
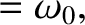
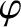
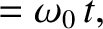
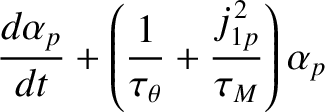
![$\displaystyle =\frac{1}{2^8\,\tau_H^{\,2}}
\left(\frac{a}{r_s}\right)^2\hat{W}_...
...^2\,\frac{[J_1(j_{1p}\,r_s/a)]^{\,2}}{[J_2(j_{1p})]^{\,2}}\,
\sin(\omega_0\,t),$](img3850.png)
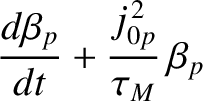
![$\displaystyle =\frac{1}{2^8\,\tau_H^{\,2}}
\left(\frac{a}{r_s}\right)^2\left(\f...
...^2\,\frac{[J_0(j_{0p}\,r_s/a)]^{\,2}}{[J_1(j_{0p})]^{\,2}}
\,\sin(\omega_0\,t).$](img3851.png)
![$\displaystyle \omega = \omega_0 -{\rm Re}\left[\sum_{p=1,\infty}\left(\hat{\alpha}_{p\,1}+\hat{\beta}_{p\,1}\right){\rm e}^{-{\rm i}\,\omega_0\,t}\right].$](img3860.png)
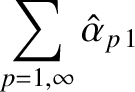
![$\displaystyle = {\rm i} \,\frac{\tau_\varphi}{2^8\,\tau_H^{\,2}}
\left(\frac{a}...
...2(j_{1p})]^{\,2}\,[(-{\rm i}\,\omega_0+1/\tau_\theta)\,\tau_M + j_{1p}^{\,2}]},$](img3862.png)
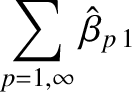
![$\displaystyle = {\rm i}\, \frac{\tau_\varphi}{2^8\,\tau_H^{\,2}}\left(\frac{a}{...
...s/a)]^{\,2}}{[J_1(j_{0p})]^{\,2}\,(-{\rm i}\,\omega_0\,\tau_M + j_{0p}^{\,2})}.$](img3864.png)
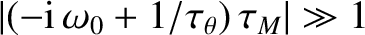 . As is clear from Table 13.2, the previous inequality is easily satisfied in a tokamak fusion reactor. Likewise,
it can be demonstrated that
in the limit that
. As is clear from Table 13.2, the previous inequality is easily satisfied in a tokamak fusion reactor. Likewise,
it can be demonstrated that
in the limit that
 . As is apparent from Table 13.2, the previous inequality is also easily satisfied in a tokamak fusion reactor. Thus, we
obtain
where
and
. As is apparent from Table 13.2, the previous inequality is also easily satisfied in a tokamak fusion reactor. Thus, we
obtain
where
and


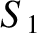



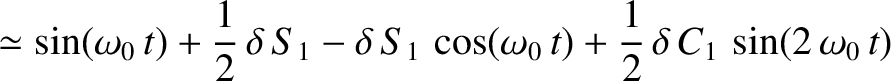
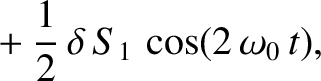
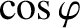
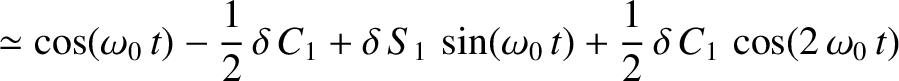
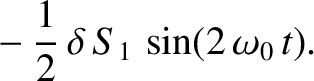
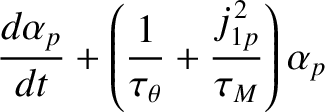
![$\displaystyle =\frac{1}{2^8\,\tau_H^{\,2}}
\left(\frac{a}{r_s}\right)^2\hat{W}_...
...}}{[J_2(j_{1p})]^{\,2}}
\left[\sin(\omega_0\,t)+\frac{1}{2}\,\delta\,S_1\right.$](img3882.png)
![$\displaystyle \phantom{=}\left.-\delta\,S_1\,\cos(\omega_0\,t)
+ \frac{1}{2}\,\...
...1\,\sin(2\,\omega_0\,t)+ \frac{1}{2}\,\delta\,S_1\,\cos(2\,\omega_0\,t)\right],$](img3883.png)
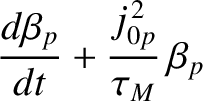
![$\displaystyle =\frac{1}{2^8\,\tau_H^{\,2}}
\left(\frac{a}{r_s}\right)^2\left(\f...
...}}{[J_1(j_{0p})]^{\,2}}
\left[\sin(\omega_0\,t)+\frac{1}{2}\,\delta\,S_1\right.$](img3884.png)
![$\displaystyle \phantom{=}\left.-\delta\,S_1\,\cos(\omega_0\,t)
+ \frac{1}{2}\,\...
...1\,\sin(2\,\omega_0\,t)+ \frac{1}{2}\,\delta\,S_1\,\cos(2\,\omega_0\,t)\right].$](img3885.png)
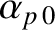
![$\displaystyle =\frac{\tau_\varphi}{2^9\,\tau_H^{\,2}}
\left(\frac{a}{r_s}\right...
..._{1p}\,r_s/a)]^{\,2}}{[J_2(j_{1p})]^{\,2}\,(\tau_M/\tau_\theta+ j_{1p}^{\,2})},$](img3889.png)
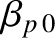
![$\displaystyle = \frac{\tau_\varphi}{2^9\,\tau_H^{\,2}}\left(\frac{a}{r_s}\right...
...ta\,S_1\,\frac{[J_0(j_{0p}\,r_s/a)]^{\,2}}{[J_1(j_{0p})]^{\,2}\, j_{0p}^{\,2}},$](img3891.png)
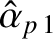
![$\displaystyle = \frac{\tau_\varphi}{2^8\,\tau_H^{\,2}}
\left(\frac{a}{r_s}\righ...
...2(j_{1p})]^{\,2}\,[(-{\rm i}\,\omega_0+1/\tau_\theta)\,\tau_M + j_{1p}^{\,2}]},$](img3892.png)

![$\displaystyle = \frac{\tau_\varphi}{2^8\,\tau_H^{\,2}}\left(\frac{a}{r_s}\right...
...s/a)]^{\,2}}{[J_1(j_{0p})]^{\,2}\,(-{\rm i}\,\omega_0\,\tau_M + j_{0p}^{\,2})},$](img3893.png)
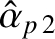
![$\displaystyle = \frac{\tau_\varphi}{2^9\,\tau_H^{\,2}}
\left(\frac{a}{r_s}\righ...
..._{1p})]^{\,2}\,[(-{\rm i}\,2\,\omega_0+1/\tau_\theta)\,\tau_M + j_{1p}^{\,2}]},$](img3895.png)
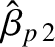
![$\displaystyle = \frac{\tau_\varphi}{2^9\,\tau_H^{\,2}}\left(\frac{a}{r_s}\right...
...)]^{\,2}}{[J_1(j_{0p})]^{\,2}\,(-{\rm i}\,2\,\omega_0\,\tau_M + j_{0p}^{\,2})}.$](img3897.png)
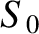
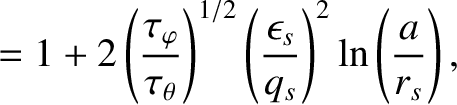

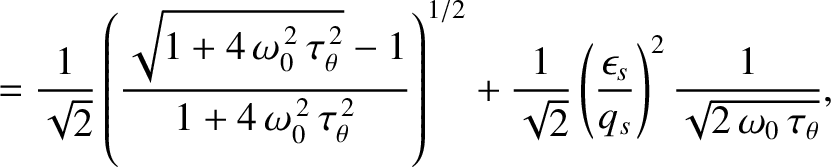
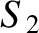

 . It is clear from Equation (13.45) that
In other words, the electromagnetic locking torque exerted by a static resonant magnetic perturbation on the rotating island chain causes an average reduction in the
chain's rotation frequency that is proportional to
. It is clear from Equation (13.45) that
In other words, the electromagnetic locking torque exerted by a static resonant magnetic perturbation on the rotating island chain causes an average reduction in the
chain's rotation frequency that is proportional to
 (i.e., to the square of the current flowing in the external magnetic field-coil that generates the perturbation). [See Equations (13.3) and (13.29).]
(i.e., to the square of the current flowing in the external magnetic field-coil that generates the perturbation). [See Equations (13.3) and (13.29).]
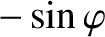 . Furthermore, as the island chain rotates past the static resonant magnetic perturbation, its rotation is alternately
accelerated (when
. Furthermore, as the island chain rotates past the static resonant magnetic perturbation, its rotation is alternately
accelerated (when
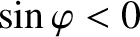 ) and decelerated (when
) and decelerated (when
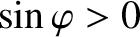 ) by this torque. However, as is apparent from the previous equation, the uneven rotation of the island chain in the presence of the perturbation [see Equation (13.45)]
causes it to spend more time in the helical phase relative to the perturbation in which it is decelerated by the torque than in the phase that it is accelerated [9,14,24,28]. This explains the net
slowing of the chain's rotation indicated in Equation (13.50).
) by this torque. However, as is apparent from the previous equation, the uneven rotation of the island chain in the presence of the perturbation [see Equation (13.45)]
causes it to spend more time in the helical phase relative to the perturbation in which it is decelerated by the torque than in the phase that it is accelerated [9,14,24,28]. This explains the net
slowing of the chain's rotation indicated in Equation (13.50).
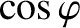 . [See Equation (13.7).] Furthermore, as the island chain rotates past the static resonant magnetic perturbation, this term alternately
destabilizes (when
. [See Equation (13.7).] Furthermore, as the island chain rotates past the static resonant magnetic perturbation, this term alternately
destabilizes (when
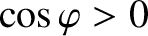 ) and stabilizes (when
) and stabilizes (when
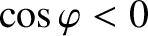 ) the chain. However, as is apparent from the previous equation, the uneven rotation of the island chain in the presence of the perturbation [see Equation (13.45)]
causes it to spend more time in the helical phase relative to the perturbation in which it is stabilized by the interaction term than in the phase that it is destabilized [9,14,24,28]. Thus, there is a net stabilizing effect when a rotating magnetic island chain interacts directly with a static resonant magnetic perturbation.
) the chain. However, as is apparent from the previous equation, the uneven rotation of the island chain in the presence of the perturbation [see Equation (13.45)]
causes it to spend more time in the helical phase relative to the perturbation in which it is stabilized by the interaction term than in the phase that it is destabilized [9,14,24,28]. Thus, there is a net stabilizing effect when a rotating magnetic island chain interacts directly with a static resonant magnetic perturbation.