Next: Locked Magnetic Island Chains Up: Mode Locking in Tokamak Previous: Analytic Solution of Phase Contents
![\includegraphics[width=\textwidth]{Chapter13/Figure13_1.eps}](img3918.png) |
Unfortunately, in the case of a rotating island chain, no further meaningful progress regarding the solution of the island phase evolution equations can be achieved via analysis. Figure 13.1 shows a numerical solution of the island phase evolution equations, (13.11)–(13.14), made for a
low-field tokamak fusion reactor (i.e., using the parameters given in the left-hand column of Table 13.2), for a case in which the mode locking parameter, 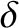 , is
ramped linearly in time. It can be seen that the numerical solution is consistent with the approximate analytic solution described in the previous section. As the
mode locking parameter increases, the electromagnetic locking torque exerted by the static resonant magnetic perturbation on the island chain causes the
chain to rotate in an increasingly irregular manner. [See Equation (13.45).] Close inspection of the figure reveals that the irregular rotation leads the island chain to spend
more time in the helical phase relative to the perturbation in which
, is
ramped linearly in time. It can be seen that the numerical solution is consistent with the approximate analytic solution described in the previous section. As the
mode locking parameter increases, the electromagnetic locking torque exerted by the static resonant magnetic perturbation on the island chain causes the
chain to rotate in an increasingly irregular manner. [See Equation (13.45).] Close inspection of the figure reveals that the irregular rotation leads the island chain to spend
more time in the helical phase relative to the perturbation in which
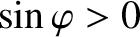 , rather than the phase in which
, rather than the phase in which
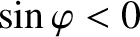 , and more time in the phase in which
, and more time in the phase in which
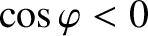 , rather than the phase in
which
, rather than the phase in
which
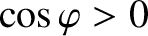 , as is consistent with Equations (13.51) and (13.52), respectively.
The distortions of the initially sinusoidal oscillations shown in the bottom two panels of Figure 13.1, as
, as is consistent with Equations (13.51) and (13.52), respectively.
The distortions of the initially sinusoidal oscillations shown in the bottom two panels of Figure 13.1, as 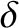 increases, are known as
mode locking distortions, and have been observed (by means of magnetic pickup coil data) in many tokamak experiments [6,14,24,28].
increases, are known as
mode locking distortions, and have been observed (by means of magnetic pickup coil data) in many tokamak experiments [6,14,24,28].
Figure 13.1 indicates that, as soon as the mode locking parameter, 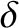 , exceeds a critical value that is of order unity, the island chain locks to the static
resonant magnetic perturbation. In other words, the island chain ceases to rotate, and, instead, maintains a fixed phase relation with respect to the perturbation.
It can be seen that the island chain locks in a helical phase relative to the perturbation such that
, exceeds a critical value that is of order unity, the island chain locks to the static
resonant magnetic perturbation. In other words, the island chain ceases to rotate, and, instead, maintains a fixed phase relation with respect to the perturbation.
It can be seen that the island chain locks in a helical phase relative to the perturbation such that
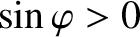 —that is, such that the electromagnetic locking torque opposes the viscous torque that
acts to maintain the chain's rotation—and
—that is, such that the electromagnetic locking torque opposes the viscous torque that
acts to maintain the chain's rotation—and
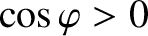 —that is, such that the resonant magnetic perturbation destabilizes the island chain [9,14,24,28].
(See Section 13.7.)
Thus, we conclude that the direct interaction of a static resonant magnetic perturbation with a magnetic island chain is stabilizing when the chain
is rotating, but becomes destabilizing as soon as the chain locks to the perturbation [9,14,24,28].
—that is, such that the resonant magnetic perturbation destabilizes the island chain [9,14,24,28].
(See Section 13.7.)
Thus, we conclude that the direct interaction of a static resonant magnetic perturbation with a magnetic island chain is stabilizing when the chain
is rotating, but becomes destabilizing as soon as the chain locks to the perturbation [9,14,24,28].
![\includegraphics[width=\textwidth]{Chapter13/Figure13_2.eps}](img3919.png) |
Figure 13.2 shows the critical value of the locking parameter, 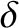 , at which a rotating island chain locks to a static resonant magnetic
perturbation, calculated as a function of the chain's natural frequency, for a low-field and a high-field tokamak fusion reactor. The calculations are made using the
parameters given in Table 13.2, except that
, at which a rotating island chain locks to a static resonant magnetic
perturbation, calculated as a function of the chain's natural frequency, for a low-field and a high-field tokamak fusion reactor. The calculations are made using the
parameters given in Table 13.2, except that  is varied. It can be seen that the critical
is varied. It can be seen that the critical 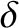 value exhibits some dependence on the exact phase at which the island
chain locks. However, this dependence becomes less marked in the physically relevant limit in which the timescale on which the locking parameter is ramped is
much longer than the rotation period of the chain (i.e., in the limit in which the ramp rate is decreaed). It can also be seen that the critical
value exhibits some dependence on the exact phase at which the island
chain locks. However, this dependence becomes less marked in the physically relevant limit in which the timescale on which the locking parameter is ramped is
much longer than the rotation period of the chain (i.e., in the limit in which the ramp rate is decreaed). It can also be seen that the critical 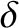 value is approximately unity, and only exhibits a fairly
weak dependence on the natural frequency,
value is approximately unity, and only exhibits a fairly
weak dependence on the natural frequency,  . Adopting the rule of thumb that
. Adopting the rule of thumb that
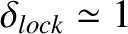 , we deduce from Equation (13.29) and Table 13.2
that that the criterion for the locking of a rotating island chain to a static resonant magnetic perturbation is
, we deduce from Equation (13.29) and Table 13.2
that that the criterion for the locking of a rotating island chain to a static resonant magnetic perturbation is