Next: Island Width Evolution Up: Mode Locking in Tokamak Previous: Numerical Solution of Phase Contents
 in Equations (13.13) and (13.14). It follows that
Making use of Equations (7.34) and (7.35), we get
in Equations (13.13) and (13.14). It follows that
Making use of Equations (7.34) and (7.35), we get
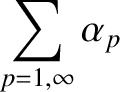 |
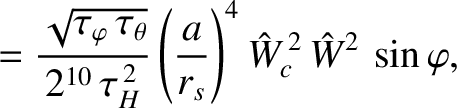 |
(13.57) |
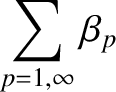 |
 |
(13.58) |
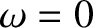 in Equation (13.11), we obtain the torque balance criterion [9]
Here, use has been made of Equations (13.29) and (13.46).
in Equation (13.11), we obtain the torque balance criterion [9]
Here, use has been made of Equations (13.29) and (13.46).
The left-hand side of the previous equation is the normalized electromagnetic locking
torque that acts to maintain a fixed helical phase relation between the island chain and the static resonant magnetic perturbation, whereas the right-hand side is the
normalized viscous torque that attempts to force the island chain to rotate with respect to the perturbation [9]. In general, the previous equation possesses two solutions.
However, only the solution in which
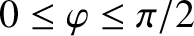 is dynamically stable [9]. Hence, we conclude that the island chain
locks in a helical phase relative to the perturbation such that
is dynamically stable [9]. Hence, we conclude that the island chain
locks in a helical phase relative to the perturbation such that
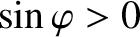 and
and
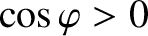 , which is consistent with the numerical simulation shown
in Figure 13.1.
, which is consistent with the numerical simulation shown
in Figure 13.1.
Actually, the previous equation only possesses solutions when
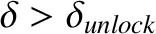 , where
, where
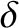 , falls below the critical value
, falls below the critical value
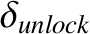 then torque balance breaks down, and the island chain
is forced to rotate with respect to the static resonant magnetic perturbation.
then torque balance breaks down, and the island chain
is forced to rotate with respect to the static resonant magnetic perturbation.
Now, making use of the data given in Table 13.2, we estimate that 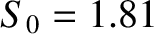 for both a low-field and a high-field tokamak fusion reactor.
It follows that
for both a low-field and a high-field tokamak fusion reactor.
It follows that
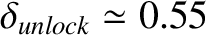 in such reactors. According to Figure 13.2, this value is about half the critical value of the locking parameter above which a rotating magnetic
island chain locks to a static resonant magnetic perturbation. In other words, once the locking parameter has exceeded the critical value required to cause a rotating island chain to
lock to a static resonant magnetic perturbation, it must be reduced by a factor of about two before the island chain will unlock from the perturbation, and start to rotate again.
This hysteresis between rotating and locked island states has been observed experimentally [14].
in such reactors. According to Figure 13.2, this value is about half the critical value of the locking parameter above which a rotating magnetic
island chain locks to a static resonant magnetic perturbation. In other words, once the locking parameter has exceeded the critical value required to cause a rotating island chain to
lock to a static resonant magnetic perturbation, it must be reduced by a factor of about two before the island chain will unlock from the perturbation, and start to rotate again.
This hysteresis between rotating and locked island states has been observed experimentally [14].
Finally, we deduce from Equations (13.29) and (13.60) and Table 13.2 that that the criterion for the unlocking of a rotating island chain from a static resonant magnetic perturbation is
 |
(13.61) |
 |
(13.62) |