Next: Bibliography Up: Mode Locking in Tokamak Previous: Locked Magnetic Island Chains Contents
 |
(13.63) |
First, let us consider a rotating magnetic island chain. Given that the island width evolves on a much longer timescale than the island phase (see Table 13.2), it is a good approximation to
replace
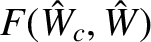 by its period average in the generalized Rutherford equation [9,10]. [See Equation (13.49).] Now,
by its period average in the generalized Rutherford equation [9,10]. [See Equation (13.49).] Now,
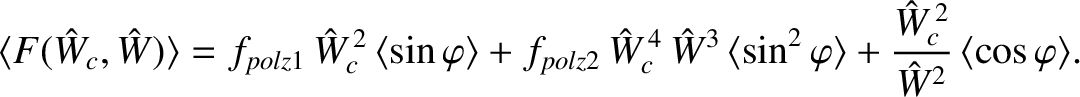 |
(13.65) |
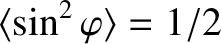 ,
,
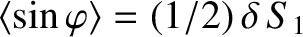 , and
, and
 . [See Equations (13.51)
and (13.52).] Thus, we obtain
. [See Equations (13.51)
and (13.52).] Thus, we obtain
 |
(13.66) |
If we use the data given in Tables 13.1 and 13.2 to estimate the sizes of the three terms on the right-hand side of the previous equation in a tokamak fusion reactor then we discover that the first two terms are completely negligible compared with the third. In other words, the polarization terms associated with the modified ion flow in the vicinity of the island chain are much smaller than the term due to the direct interaction between the island chain and the static resonant magnetic perturbation. In this limit, we can use Equation (13.29) to write
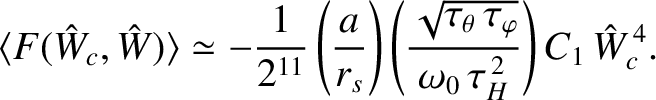 |
(13.67) |
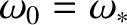 ), and
in a high-field tokamak fusion reactor. Of course, these estimates are only valid as long as the locking criteria (13.53) and (13.54) are not satisfied. Equations (13.53), (13.54),
(13.68), and (13.69) suggest that the stabilizing effect of the interaction of a rotating magnetic island chain with a
static resonant magnetic perturbation could completely stabilize a relatively narrow island chain, but would not be able to completely stabilize a wide island chain, because the chain would lock to the perturbation before complete stabilization was acheived.
The complete stabilization of a narrow rotating magnetic island chain by a static resonant magnetic perturbation has been observed experimentally [16].
), and
in a high-field tokamak fusion reactor. Of course, these estimates are only valid as long as the locking criteria (13.53) and (13.54) are not satisfied. Equations (13.53), (13.54),
(13.68), and (13.69) suggest that the stabilizing effect of the interaction of a rotating magnetic island chain with a
static resonant magnetic perturbation could completely stabilize a relatively narrow island chain, but would not be able to completely stabilize a wide island chain, because the chain would lock to the perturbation before complete stabilization was acheived.
The complete stabilization of a narrow rotating magnetic island chain by a static resonant magnetic perturbation has been observed experimentally [16].
Let us now consider a locked magnetic island chain. Equations (13.59), (13.60), and (13.64) yield
![$\displaystyle F(\hat{W}_c,\hat{W}) = f_{polz1}\left(\frac{\delta_{unlock}}{\del...
...delta_{unlock}}{\delta}\right)^2\right]^{1/2}\frac{\hat{W}_c^{\,2}}{\hat{W}^2}.$](img3953.png) |
(13.70) |
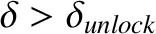 (i.e., provided that the island chain remains locked to the static
resonant magnetic perturbation). Assuming that
(i.e., provided that the island chain remains locked to the static
resonant magnetic perturbation). Assuming that
 ,
,
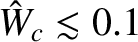 , and
, and
 , it is clear from the data given in Table 13.1 that the
first two terms on the right-hand side of the previous equation are completely negligible compared to the third. In other words, just as is the case for a rotating island chain, the polarization terms in the Rutherford equation associated with the modified ion flow in the vicinity of the island chain
are much smaller than the term due to the direct interaction between the island chain and the static resonant magnetic perturbation. In this case, we can write
, it is clear from the data given in Table 13.1 that the
first two terms on the right-hand side of the previous equation are completely negligible compared to the third. In other words, just as is the case for a rotating island chain, the polarization terms in the Rutherford equation associated with the modified ion flow in the vicinity of the island chain
are much smaller than the term due to the direct interaction between the island chain and the static resonant magnetic perturbation. In this case, we can write
![$\displaystyle F(\hat{W}_c,\hat{W}) \simeq \left[1- \left(\frac{\delta_{unlock}}{\delta}\right)^2\right]^{1/2}\left(\frac{\hat{W}_c}{\hat{W}}\right)^2.$](img3957.png) |
(13.71) |
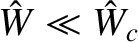 . This destabilizing effect has been observed experimentally [14].
. This destabilizing effect has been observed experimentally [14].
Finally, experiments have been performed in which the rotation frequency of a magnetic island chain in a tokamak plasma is controlled by locking the chain to a rotating resonant magnetic perturbation [23]. More ambitious experiments have been performed in which the helical phase of a rotating resonant magnetic perturbation is actively controlled in such a manner that a magnetic island chain in a tokamak plasma is held in a permanent stabilizing phase relation with respect to the perturbation [19,21]. Unfortunately, neither of these control schemes is practical in a tokamak fusion reactor because the magnetic field-coils that generate the rotating magnetic perturbation would have to be placed inside the vacuum vessel (otherwise the oscillating magnetic field generated by the coils would be shielded from the plasma by eddy currents excited in the vessel), where they would be unacceptably vulnerable to neutrons produced by fusion reactions within the plasma, as well as large electromagnetic forces generated by plasma disruptions.