Magnetic Field-Line Curvature
As was mentioned in Section 1.14, the bootstrap current has a destabilizing effect on wide magnetic island chains [2,5,16].
It turns out that the mean curvature of magnetic field-lines in the inner region has a stabilizing effect on such chains that is similar in magnitude to the destabilizing effect of the bootstrap current [11,15]. Hence, it is
not consistent to include the bootstrap current in our analysis without also including curvature effects. The appropriate
curvature terms are derived in Reference [13]. We shall simply incorporate them into our model,
which generalizes to give:
Here,
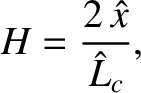 |
(11.56) |
and
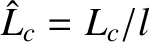 , where
, where
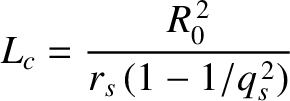 |
(11.57) |
is the magnetic curvature length (i.e., the mean radius of curvature of magnetic field-lines at the rational surface) [12,17].
Note that the previous expression for 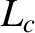 is only valid in a large-aspect ratio, low-
is only valid in a large-aspect ratio, low-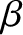 plasma with circular magnetic flux-surfaces. A more general
expression is given in Section A.8.
plasma with circular magnetic flux-surfaces. A more general
expression is given in Section A.8.
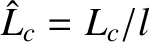 , where
is the magnetic curvature length (i.e., the mean radius of curvature of magnetic field-lines at the rational surface) [12,17].
Note that the previous expression for
, where
is the magnetic curvature length (i.e., the mean radius of curvature of magnetic field-lines at the rational surface) [12,17].
Note that the previous expression for 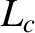 is only valid in a large-aspect ratio, low-
is only valid in a large-aspect ratio, low-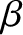 plasma with circular magnetic flux-surfaces. A more general
expression is given in Section A.8.
plasma with circular magnetic flux-surfaces. A more general
expression is given in Section A.8.