Next: Tearing Modes in Toroidal Up: Introduction Previous: Error-Field Penetration Contents
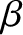 values in tokamak plasmas that are adequate for the achievement of
thermonuclear fusion [7,37,52]. However, a magnetic island chain can only locally flatten
the plasma pressure when its radial width exceeds a certain threshold value that depends on the local ratio of the
parallel and perpendicular energy diffusivities [19]. This observation leads to the conclusion that neoclassical tearing modes are actually meta-stable.
In other words, some sort of seed perturbation must be applied to the relevant rational magnetic flux-surface in order to trigger a neoclassical tearing mode.
In practice, the seed perturbation usually takes the form of a transient magnetic perturbation that is resonant at the
rational surface [31]. Such perturbations arise naturally in tokamak plasmas as a consequence of plasma instabilities such as internal kink modes and edge localized modes [64]. Neoclassical tearing modes can be stabilized by driving a parallel (to the magnetic field) current in the vicinity of the rational surface by means of electron cyclotron waves
injected into the plasma; the idea is to fill in the helical hole in the bootstrap current profile [30,38,46,49,69,70]. (See Chapter 12.)
values in tokamak plasmas that are adequate for the achievement of
thermonuclear fusion [7,37,52]. However, a magnetic island chain can only locally flatten
the plasma pressure when its radial width exceeds a certain threshold value that depends on the local ratio of the
parallel and perpendicular energy diffusivities [19]. This observation leads to the conclusion that neoclassical tearing modes are actually meta-stable.
In other words, some sort of seed perturbation must be applied to the relevant rational magnetic flux-surface in order to trigger a neoclassical tearing mode.
In practice, the seed perturbation usually takes the form of a transient magnetic perturbation that is resonant at the
rational surface [31]. Such perturbations arise naturally in tokamak plasmas as a consequence of plasma instabilities such as internal kink modes and edge localized modes [64]. Neoclassical tearing modes can be stabilized by driving a parallel (to the magnetic field) current in the vicinity of the rational surface by means of electron cyclotron waves
injected into the plasma; the idea is to fill in the helical hole in the bootstrap current profile [30,38,46,49,69,70]. (See Chapter 12.)