Figure 14.1 shows contours of the poloidal magnetic flux for a typical plasma discharge in the KSTAR tokamak [42].
It can be seen that there are a number of differences from the idealized tokamak pictured in Figure 1.5. The first main difference
is that the flux-surfaces in Figure 14.1 do not have circular cross-sections. In particular, the flux-surfaces are highly vertically elongated. It turns out
that this feature allows the toroidal plasma current driven in a tokamak discharge to be increased without violating the Kruskal-Shafranov
criterion. (See Section 1.10.) Hence, all modern tokamaks have strongly-shaped, vertically-elongated cross-sections. The second main difference is that the edge of the plasma is defined by a last closed
magnetic flux-surface that features a magnetic X-point (i.e., a hyperbolic null in the poloidal magnetic field). Plasma that crosses the last closed flux-surface is rapidly conducted along magnetic
field-lines, in a thin scrape-off layer, to divertor plates located below the plasma. The purpose of this feature is to mitigate the interaction of the
plasma with the plasma-facing components, and, thereby, help limit the flux of impurities into the plasma [44]. Hence, all modern tokamaks have magnetic X-points. Given that the poloidal magnetic field-strength
at the X-point is zero, the safety-factor value on the last closed flux-surface is infinite. [See Equation (1.76).] Experimentally, it is found that the safety-factor value
on the magnetic flux-surface that encloses 95% of the poloidal magnetic flux enclosed by the last closed flux-surface, which is known as 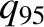 , plays an
analogous role to the edge safety-factor value,
, plays an
analogous role to the edge safety-factor value, 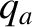 , in a tokamak without a magnetic X-point [64]. (See Section 14.4.) Thus, the rule of thumb for safe operation,
, in a tokamak without a magnetic X-point [64]. (See Section 14.4.) Thus, the rule of thumb for safe operation,
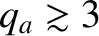 ,
is replaced by
,
is replaced by
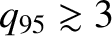 . (See Section 1.9.)
. (See Section 1.9.)
In the type of highly-shaped plasma equilibrium pictured in Figure 14.1, tearing modes with the same toroidal mode number, but different poloidal mode numbers, are coupled together [13,23]. Somewhat confusingly, this effect is known as toroidal mode coupling. Toroidal mode coupling allows magnetic island
chains resonant on different rational surfaces within the plasma to interact. The interaction is expected to be mutually destabilizing [23]. However, sheared plasma
rotation acts to prevent such interaction. (See Chapter 14.)
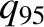 , plays an
analogous role to the edge safety-factor value,
, plays an
analogous role to the edge safety-factor value, 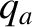 , in a tokamak without a magnetic X-point [64]. (See Section 14.4.) Thus, the rule of thumb for safe operation,
, in a tokamak without a magnetic X-point [64]. (See Section 14.4.) Thus, the rule of thumb for safe operation,
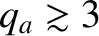 ,
is replaced by
,
is replaced by
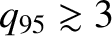 . (See Section 1.9.)
. (See Section 1.9.)