Next: Example Tokamak Discharge Up: Toroidal Tearing Modes Previous: Calculation of Inductance Matrix Contents
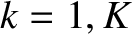 [see Equation (14.112)], can also be written in the form [6,14]
for
[see Equation (14.112)], can also be written in the form [6,14]
for 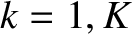 ,
where the E-matrix,
,
where the E-matrix, 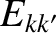 , is the inverse of the F-matrix. Because the F-matrix is Hermitian, so is the
E-matrix. Given that the F-matrix is a dimensionless inductance matrix, it is clear that the E-matrix is a dimensionless
reluctance matrix.
, is the inverse of the F-matrix. Because the F-matrix is Hermitian, so is the
E-matrix. Given that the F-matrix is a dimensionless inductance matrix, it is clear that the E-matrix is a dimensionless
reluctance matrix.
In cylindrical geometry, the tearing mode dispersion relation takes the form
for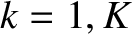 . [See Equation (3.74).] Here,
. [See Equation (3.74).] Here, 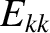 is the tearing stability index at the
is the tearing stability index at the  th rational surface [20]. A comparison
between the previous two equations reveals that the main difference between the tearing mode dispersion relation in
toroidal geometry, and that in cylindrical geometry, is the presence of non-zero off-diagonal elements of the
E-matrix in the former case. These off-diagonal elements couple different poloidal harmonics.
th rational surface [20]. A comparison
between the previous two equations reveals that the main difference between the tearing mode dispersion relation in
toroidal geometry, and that in cylindrical geometry, is the presence of non-zero off-diagonal elements of the
E-matrix in the former case. These off-diagonal elements couple different poloidal harmonics.
The non-zero off-diagonal elements of the E-matrix are a consequence of non-zero off-diagonal elements of the F-matrix. (If the F-matrix were diagonal then the E-matrix would also be diagonal). The off-diagonal elements of the F-matrix are determined by double integrals of the form (14.113) in which the normalized mutual inductances of current sheets flowing parallel to the local equilibrium magnetic field at different rational magnetic flux-surfaces are calculated. For the case of a cylindrical plasma, the rational surfaces are concentric cylindrical surfaces of circular cross-section, and the current sheets have different poloidal periods. Consequently, the mutual inductance integrals all average to zero. The same is not true, in general, in a toroidal plasma, for two reasons. First, in a toroidal plasma, the different rational magnetic flux-surfaces are not concentric, as a consequence of toroidicity and pressure gradients [19,34]. (See Figure 14.1.) This effect, which is known as the Shafranov shift [34], gives rise to a coupling between poloidal harmonics whose poloidal mode numbers differ by unity [5,14]. Second, in a realistic tokamak plasma, the rational magnetic flux-surfaces do not have circular cross-sections. Instead, they are highly elongated in the vertical direction, and slightly triangular. (See Figure 14.1.) These shaping effects give rise to coupling between poloidal harmonics whose poloidal mode numbers differ by two and three, respectively [14]. Of course, there is no coupling between toroidal harmonics with different toroidal mode numbers because the rational magnetic flux-surfaces are all axisymmetric. This accounts for the fact that a general toroidal tearing mode possesses a unique toroidal mode number, but does not possess a unique poloidal mode number.
Suppose that a toroidal tearing mode reconnects an amount of magnetic flux,
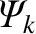 , at the
, at the
 th rational surface, and generates a current sheet of normalized strength,
th rational surface, and generates a current sheet of normalized strength,
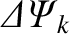 at the same surface. What is the response of the other rational surfaces in the plasma? In fact, the
response at the
at the same surface. What is the response of the other rational surfaces in the plasma? In fact, the
response at the 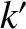 th rational surface (where
th rational surface (where  ) can fall between two extremes. Either the response can be such that a
current sheet is induced at the
) can fall between two extremes. Either the response can be such that a
current sheet is induced at the 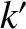 th rational surface that completely suppresses driven magnetic reconnection at
the surface (i.e.,
th rational surface that completely suppresses driven magnetic reconnection at
the surface (i.e.,
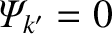 ), or the response can be such that no current sheet is induced at the
), or the response can be such that no current sheet is induced at the
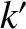 th rational surface (i.e.,
th rational surface (i.e.,
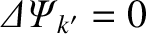 ), and the maximum amount of reconnection is driven at the
surface. We shall refer to the first type of response as full shielding, and to the second type as a
no shielding.
), and the maximum amount of reconnection is driven at the
surface. We shall refer to the first type of response as full shielding, and to the second type as a
no shielding.
Suppose that the response at all of the other rational surfaces in the plasma is of the full shielding type: that is,
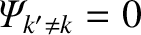 . It follows from Equation (14.119) that [14]
. It follows from Equation (14.119) that [14]
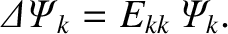 |
(14.121) |
![\includegraphics[width=0.6\textwidth]{Chapter14/Figure14_1.eps}](img4215.png)
|
Suppose that the response at all of the other rational surfaces in the plasma is of the no shielding type: that is,
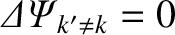 . It follows from Equation (14.118) that [14]
. It follows from Equation (14.118) that [14]
 |
(14.122) |
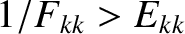 [14]. In other words, we expect the mutual
coupling of the different resonant surfaces in the plasma, in the absence of shielding, to destabilize the tearing mode relative to the case in which there is
full shielding.
[14]. In other words, we expect the mutual
coupling of the different resonant surfaces in the plasma, in the absence of shielding, to destabilize the tearing mode relative to the case in which there is
full shielding.
The question that we now need to address is which of the two extreme response regimes just outlined most accurately describes a tearing mode in a realistic tokamak plasma. In order to determine the answer to this question, let us examine an example tokamak discharge.