Calculation of Inductance Matrix
In principle, we could determine the relationship between
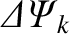 and the
and the
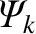 (which is equivalent to determining the relationship between the
(which is equivalent to determining the relationship between the 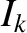 and the
and the
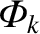 ) by solving Equations (14.46) and (14.47) subject to suitable spatial boundary conditions at
) by solving Equations (14.46) and (14.47) subject to suitable spatial boundary conditions at  and
and 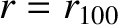 [11,14,22]. However, in this chapter, we shall adopt a more direct approach [12,13,15,16].
[11,14,22]. However, in this chapter, we shall adopt a more direct approach [12,13,15,16].
According to the Biot-Savart law [27]:
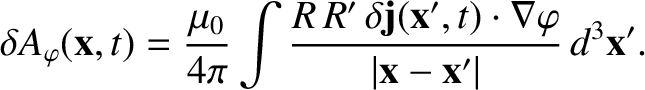 |
(14.102) |
Let us assume that
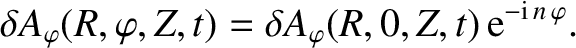 |
(14.103) |
It follows that we can evaluate the integral on the right-hand side of Equation (14.102) at 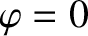 without loss of generality. Now,
without loss of generality. Now,
 |
(14.104) |
so we get
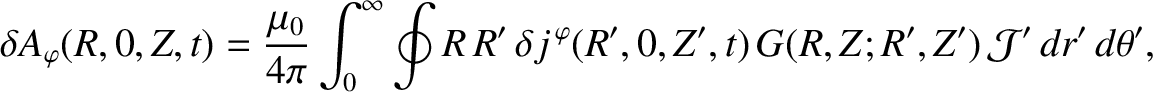 |
(14.105) |
where
![$\displaystyle G(R,Z;R',Z') = \frac{1}{2}\oint \frac{\left(\cos[(n-1)\,\varphi']...
...arphi'}{\left[R^{2}+R'^{\,2} +(Z-Z')^{2} -2\,R\,R'\,\cos\varphi'\right]^{1/2}}.$](img4181.png) |
(14.106) |
Finally, making use of the standard definition of a toroidal
function [23],
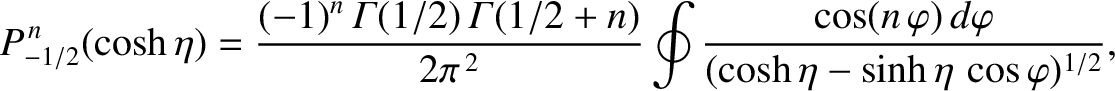 |
(14.107) |
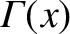 denotes a gamma function [1],
we arrive at
where
denotes a gamma function [1],
we arrive at
where
![$\displaystyle \eta = \tanh^{-1}\left[\frac{2\,R\,R'}{R^{2}+R'^{\,2}+(Z-Z')^{2}}\right].$](img4187.png) |
(14.109) |
According to Equations (14.60) and (14.66),
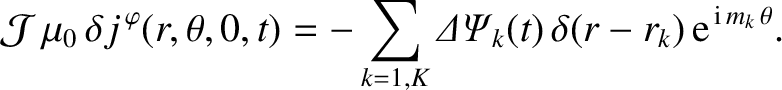 |
(14.110) |
Furthermore, Equations (14.65) and (14.78) yield
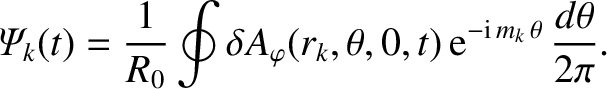 |
(14.111) |
Hence, combining the previous two expressions with Equation (14.105), we obtain the expected normalized inductance
relation [see Equation (14.94)],
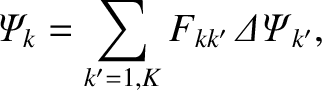 |
(14.112) |
for 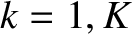 ,
where [12,13,15,16]
,
where [12,13,15,16]
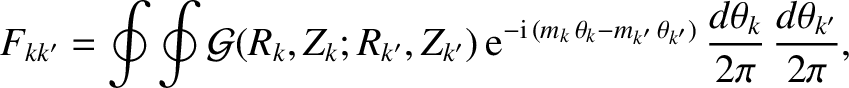 |
(14.113) |
and
with
![$\displaystyle \eta_{kk'} = \tanh^{-1}\left[\frac{2\,R_k\,R_{k'}}{R_k^{\,2}+R_{k'}^{\,2}+(Z_k-Z_{k'})^{2}}\right].$](img4194.png) |
(14.115) |
Here,  and
and 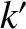 index the various rational surfaces in the plasma. Moreover, the double integral in Equation (14.113) is taken around the
index the various rational surfaces in the plasma. Moreover, the double integral in Equation (14.113) is taken around the  th rational surface (cylindrical coordinates
th rational surface (cylindrical coordinates 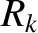 , 0,
, 0, 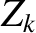 ; flux coordinates
; flux coordinates 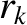 ,
, 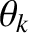 , 0, with
, 0, with 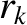 constant; resonant poloidal mode number
constant; resonant poloidal mode number  ) and the
) and the 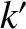 th rational surface (cylindrical coordinates
th rational surface (cylindrical coordinates 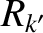 , 0,
, 0, 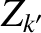 ; flux coordinates
; flux coordinates 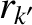 ,
,
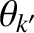 , 0, with
, 0, with 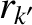 constant; resonant poloidal mode number
constant; resonant poloidal mode number  ).
).
Note that
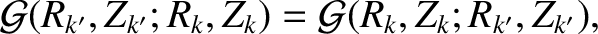 |
(14.116) |
which, from Equation (14.113), implies that the F-matrix is Hermitian [see Equation (14.100)], as must be the case.
Finally, according to Equations (14.95) and (14.113), the unnormalized inductance matrix
takes the form
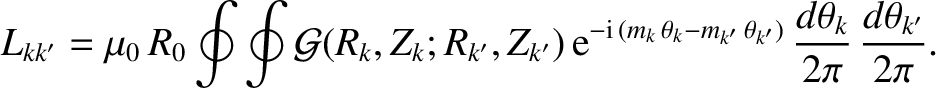 |
(14.117) |
The Hermitian L-matrix,  , specifies the self and mutual inductances of the helical current sheets that flow at the various
rational surfaces within the plasma.
, specifies the self and mutual inductances of the helical current sheets that flow at the various
rational surfaces within the plasma.
Note that the calculation of the F-matrix outlined in this section is only approximate. The exact calculation is specified in
References [11] and [22].
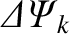 and the
and the
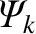 (which is equivalent to determining the relationship between the
(which is equivalent to determining the relationship between the 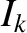 and the
and the
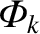 ) by solving Equations (14.46) and (14.47) subject to suitable spatial boundary conditions at
) by solving Equations (14.46) and (14.47) subject to suitable spatial boundary conditions at  and
and 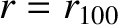 [11,14,22]. However, in this chapter, we shall adopt a more direct approach [12,13,15,16].
[11,14,22]. However, in this chapter, we shall adopt a more direct approach [12,13,15,16].
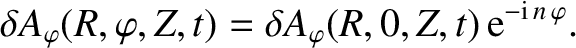
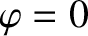 without loss of generality. Now,
without loss of generality. Now,

![$\displaystyle G(R,Z;R',Z') = \frac{1}{2}\oint \frac{\left(\cos[(n-1)\,\varphi']...
...arphi'}{\left[R^{2}+R'^{\,2} +(Z-Z')^{2} -2\,R\,R'\,\cos\varphi'\right]^{1/2}}.$](img4181.png)
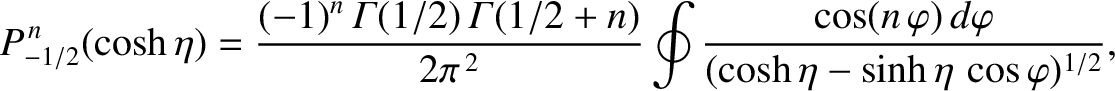
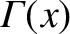 denotes a gamma function [1],
we arrive at
denotes a gamma function [1],
we arrive at
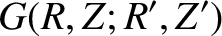
![$\displaystyle = \frac{(-1)^{n+1}\,\pi^{2}}{{\mit\Gamma}(1/2)\,{\mit\Gamma}(n+1/2)}
\left[\frac{\cosh\eta}{R^{2}+R'^{\,2}+(Z-Z')^{2}}\right]^{1/2}$](img4185.png)
![$\displaystyle \phantom{=}\times\left[(n-1/2)\,P_{-1/2}^{\,n-1}(\cosh\eta)+
\frac{P_{-1/2}^{\,n+1}(\cosh\eta)}{n+1/2}\right],$](img4186.png)
![$\displaystyle \eta = \tanh^{-1}\left[\frac{2\,R\,R'}{R^{2}+R'^{\,2}+(Z-Z')^{2}}\right].$](img4187.png)
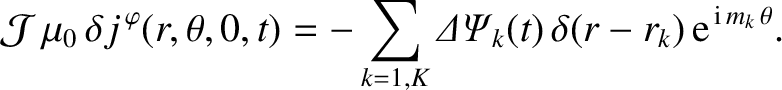
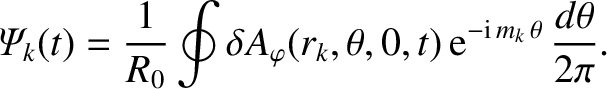
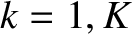 ,
where [12,13,15,16]
and
,
where [12,13,15,16]
and
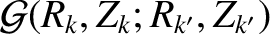
![$\displaystyle = \frac{(-1)^{n}\,\pi^{2}\,R_k\,R_{k'}/R_0}{2\,{\mit\Gamma}(1/2)\...
...ft[\frac{\cosh\eta_{kk'}}{R_k^{\,2}+R_{k'}^{\,2}+(Z_k-Z_{k'})^{2}}\right]^{1/2}$](img4192.png)
![$\displaystyle \phantom{=}\times\left[(n-1/2)\,P_{-1/2}^{\,n-1}(\cosh\eta_{kk'})+
\frac{P_{-1/2}^{\,n+1}(\cosh\eta_{kk'})}{n+1/2}\right],$](img4193.png)
![$\displaystyle \eta_{kk'} = \tanh^{-1}\left[\frac{2\,R_k\,R_{k'}}{R_k^{\,2}+R_{k'}^{\,2}+(Z_k-Z_{k'})^{2}}\right].$](img4194.png)
 and
and 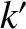 index the various rational surfaces in the plasma. Moreover, the double integral in Equation (14.113) is taken around the
index the various rational surfaces in the plasma. Moreover, the double integral in Equation (14.113) is taken around the  th rational surface (cylindrical coordinates
th rational surface (cylindrical coordinates 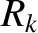 , 0,
, 0, 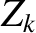 ; flux coordinates
; flux coordinates 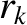 ,
, 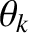 , 0, with
, 0, with 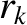 constant; resonant poloidal mode number
constant; resonant poloidal mode number  ) and the
) and the 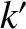 th rational surface (cylindrical coordinates
th rational surface (cylindrical coordinates 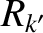 , 0,
, 0, 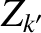 ; flux coordinates
; flux coordinates 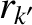 ,
,
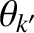 , 0, with
, 0, with 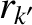 constant; resonant poloidal mode number
constant; resonant poloidal mode number  ).
).
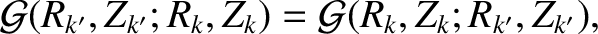
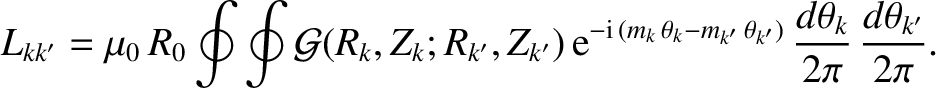
 , specifies the self and mutual inductances of the helical current sheets that flow at the various
rational surfaces within the plasma.
, specifies the self and mutual inductances of the helical current sheets that flow at the various
rational surfaces within the plasma.