Next: Magnetic Island Chains Up: Toroidal Tearing Modes Previous: Perturbed Current Density Contents
 |
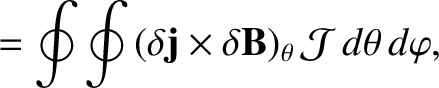 |
(14.61) |
 |
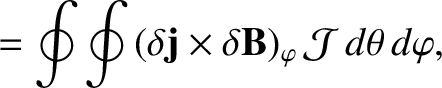 |
(14.62) |
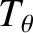 |
![$\displaystyle = - \frac{2\pi^2\,R_0}{\mu_0}\sum_{k=1,K}{\rm Im}\left([\chi_k]_{r_{k-}}^{r_{k+}}\,\psi_k^{\,\ast}\right)\,\delta(r-r_k),$](img4100.png) |
(14.63) |
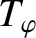 |
![$\displaystyle = \frac{2\pi^2\,R_0}{\mu_0}\sum_{k=1,K}{\rm Im}\left(\frac{n}{m_k}\,[\chi_k]_{r_{k-}}^{r_{k+}}\,\psi_k^{\,\ast}\right)\,\delta(r-r_k).$](img4102.png) |
(14.64) |
Let
Note that these quantities are, in general, complex. It follows that [11,14,16]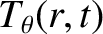 |
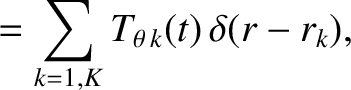 |
(14.67) |
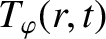 |
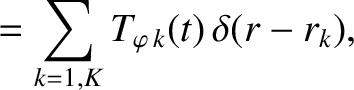 |
(14.68) |
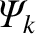 is the reconnected magnetic flux at the
is the reconnected magnetic flux at the
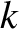 th rational surface, whereas
th rational surface, whereas
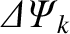 parameterizes the amplitude and phase of the current sheet flowing (parallel to the equilibrium
magnetic field) at the same surface.
parameterizes the amplitude and phase of the current sheet flowing (parallel to the equilibrium
magnetic field) at the same surface.