Next: Useful Identities Up: Toroidal Tearing Modes Previous: Introduction Contents
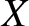 ,
, 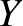 ,
, 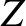 be a conventional right-handed Cartesian coordinate system (where
be a conventional right-handed Cartesian coordinate system (where 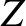 measures vertical height).
measures vertical height).
Let 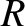 ,
,  ,
, 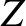 be the corresponding
cylindrical coordinate system, where
be the corresponding
cylindrical coordinate system, where
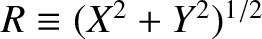 and
and
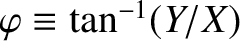 .
It follows that
.
It follows that
Finally, let us define a flux coordinate system: 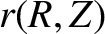 ,
,
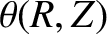 ,
,  , where [5,14]
, where [5,14]
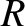 ,
, 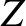 ,
,  ,
,  are the same as the corresponding quantities defined in Section 2.10.)
Here,
are the same as the corresponding quantities defined in Section 2.10.)
Here,  is a convenient scale major radius, the magnetic flux-surface label
is a convenient scale major radius, the magnetic flux-surface label  has units of length, and
has units of length, and  is
is an angular coordinate that increases by
is
is an angular coordinate that increases by  radians for every poloidal circuit of the magnetic axis. Let
radians for every poloidal circuit of the magnetic axis. Let  correspond to the magnetic axis of the plasma, and let
correspond to the magnetic axis of the plasma, and let 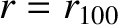 correspond to the last closed magnetic flux-surface. Suppose that
correspond to the last closed magnetic flux-surface. Suppose that 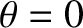 on the outboard midplane of the plasma. It follows that
on the outboard midplane of the plasma. It follows that
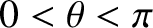 below the midplane.
below the midplane.