Next: Electromagnetic Torques Up: Toroidal Tearing Modes Previous: Perturbed Magnetic Field Contents
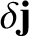 be the perturbed current density associated with the tearing mode. We can write
be the perturbed current density associated with the tearing mode. We can write
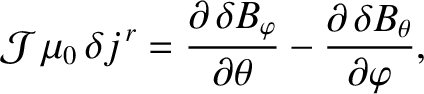 |
(14.55) |
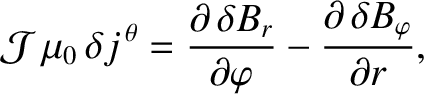 |
(14.56) |
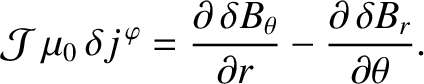 |
(14.57) |
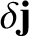 are zero. Consider, however, the
behavior in the vicinity of the
are zero. Consider, however, the
behavior in the vicinity of the  th rational surface,
th rational surface, 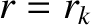 , at which
, at which
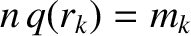 . (See Section 3.7.) In general,
. (See Section 3.7.) In general, 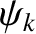 ,
,
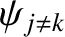 , and
, and
 are continuous across the surface, whereas
are continuous across the surface, whereas 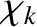 is discontinuous [11,14].
Hence, we deduce that
where use has been made of Equations (14.45) and (14.54). Here, it is assumed that there are
is discontinuous [11,14].
Hence, we deduce that
where use has been made of Equations (14.45) and (14.54). Here, it is assumed that there are 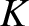 rational surfaces in the plasma,
numbered sequentially from 1 to
rational surfaces in the plasma,
numbered sequentially from 1 to 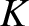 , in the order of the innermost to the outermost. It is easily demonstrated from Equations (14.7)–(14.9), (14.19)–(14.22),
and (14.58)–(14.60) that
, in the order of the innermost to the outermost. It is easily demonstrated from Equations (14.7)–(14.9), (14.19)–(14.22),
and (14.58)–(14.60) that
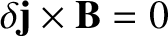 at a given rational surface. Thus, we conclude that a current sheet forms at
each rational surface in the plasma. Moreover, each sheet is made up of current filaments that flow parallel to the local equilibrium magnetic field.
at a given rational surface. Thus, we conclude that a current sheet forms at
each rational surface in the plasma. Moreover, each sheet is made up of current filaments that flow parallel to the local equilibrium magnetic field.