Next: Equilibrium Plasma Current Density Up: Toroidal Tearing Modes Previous: Useful Identities Contents
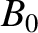 is a convenient scale magnetic field-strength,
and
is the safety-factor profile. [See Equation (2.128).]
Here,
is a convenient scale magnetic field-strength,
and
is the safety-factor profile. [See Equation (2.128).]
Here, 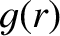 and
and 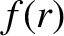 are dimensionless functions.
are dimensionless functions.
It follows from Equations (14.1)–(14.5), (14.17), and (14.18) that
The equilibrium poloidal magnetic flux (divided by  ),
),
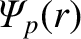 , satisfies,
, satisfies,
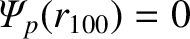 . [Note that
. [Note that
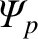 is equivalent to the quantity
is equivalent to the quantity  defined in Equation (2.130).] The normalized poloidal magnetic
flux,
defined in Equation (2.130).] The normalized poloidal magnetic
flux,
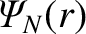 , is defined such that
, is defined such that
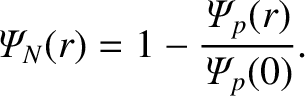 |
(14.26) |
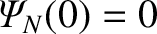 and
and
 . In general,
. In general,
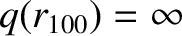 . Finally, if
. Finally, if
 then
then
 . Thus,
. Thus, 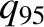 is the safety-factor of the magnetic flux-surface that encloses 95% of the poloidal magnetic flux enclosed by
the last closed magnetic flux-surface.
is the safety-factor of the magnetic flux-surface that encloses 95% of the poloidal magnetic flux enclosed by
the last closed magnetic flux-surface.