Next: Calculation of Inductance Matrix Up: Toroidal Tearing Modes Previous: Magnetic Island Chains Contents
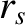 , satisfies
, satisfies
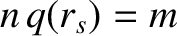 , where
, where  and
and 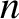 are the unique poloidal and toroidal mode numbers, respectively, of the mode. We also found that the mode reconnects magnetic flux
at the rational surface, and simultaneously generates a current sheet at the surface that flows parallel to the local magnetic field.
are the unique poloidal and toroidal mode numbers, respectively, of the mode. We also found that the mode reconnects magnetic flux
at the rational surface, and simultaneously generates a current sheet at the surface that flows parallel to the local magnetic field.
In this chapter, we started to investigate a tearing mode in a toroidal
tokamak plasma. We found that such a mode possesses a unique toroidal mode number, but consists of many coupled poloidal harmonics. [See Equations (14.46) and (14.47).]
Moreover, the mode resonates at multiple rational surfaces lying within the plasma. The  th rational surface, minor radius
th rational surface, minor radius 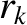 , satisfies
, satisfies
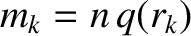 , where
, where  is a positive
integer. In principle, the mode can reconnect magnetic flux at each rational surface in the plasma, and can also generate a current sheet, flowing parallel to
the equilibrium magnetic field, at each surface. We wish to find the relationship between the reconnected magnetic fluxes and the current sheet strengths at the various
rational surfaces in the plasma.
is a positive
integer. In principle, the mode can reconnect magnetic flux at each rational surface in the plasma, and can also generate a current sheet, flowing parallel to
the equilibrium magnetic field, at each surface. We wish to find the relationship between the reconnected magnetic fluxes and the current sheet strengths at the various
rational surfaces in the plasma.
Let
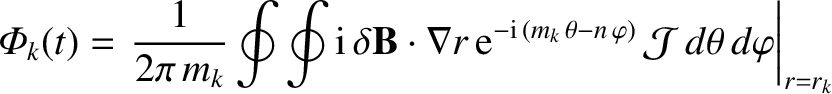 |
(14.89) |
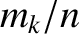 helical component of the radial magnetic flux at the
helical component of the radial magnetic flux at the  th rational surface. It follows from Equations (14.2)–(14.4), (14.44), and (14.65) that
Thus,
th rational surface. It follows from Equations (14.2)–(14.4), (14.44), and (14.65) that
Thus,
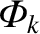 is related to the reconnected magnetic flux,
is related to the reconnected magnetic flux,
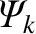 (which is actually a flux per unit length), at the
(which is actually a flux per unit length), at the  th rational surface.
Let
th rational surface.
Let
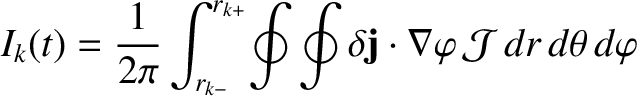 |
(14.91) |
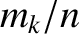 helical component of the localized toroidal plasma current flowing at the
helical component of the localized toroidal plasma current flowing at the  th rational surface. It follows from Equations (14.2)–(14.4), (14.60), and
(14.66) that
Thus,
th rational surface. It follows from Equations (14.2)–(14.4), (14.60), and
(14.66) that
Thus, 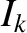 is related to the parallel current sheet strength,
is related to the parallel current sheet strength,
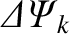 , at the
, at the  th rational surface.
th rational surface.
In general, we expect the
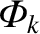 and the
and the 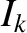 to be related to one another via a complex inductance matrix:
to be related to one another via a complex inductance matrix:
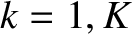 . Equations (14.90), (14.92), and (14.93) yield [6,14]
where
Hence, we deduce that the complex matrix,
. Equations (14.90), (14.92), and (14.93) yield [6,14]
where
Hence, we deduce that the complex matrix, 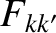 , which relates the reconnected fluxes to the current sheet strengths at the various rational surfaces within the plasma, can
be regarded as a dimensionless inductance matrix.
, which relates the reconnected fluxes to the current sheet strengths at the various rational surfaces within the plasma, can
be regarded as a dimensionless inductance matrix.
The magnetic energy associated with the tearing perturbation is written
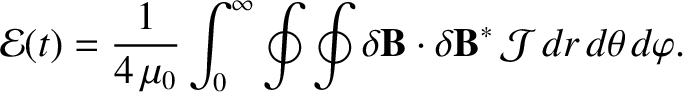 |
(14.96) |
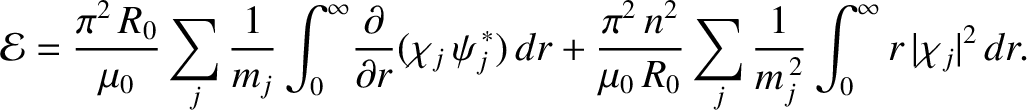 |
(14.97) |
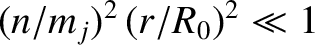 .
Now, we expect
.
Now, we expect
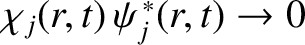 as
as
 . Furthermore, assuming that the plasma is isolated (i.e., it is not interacting with a resistive wall, or an externally generated resonant magnetic perturbation), we also expect
. Furthermore, assuming that the plasma is isolated (i.e., it is not interacting with a resistive wall, or an externally generated resonant magnetic perturbation), we also expect
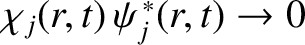 as
as
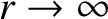 .
Recalling, however, that
.
Recalling, however, that
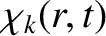 is discontinuous across the
is discontinuous across the  th rational surface, whereas the
th rational surface, whereas the
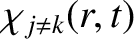 and the
and the
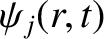 are continuous, and making use of Equations (14.65), (14.66),
(14.90), and (14.92),
we arrive at
are continuous, and making use of Equations (14.65), (14.66),
(14.90), and (14.92),
we arrive at
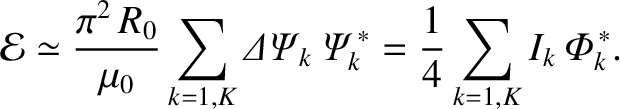 |
(14.98) |
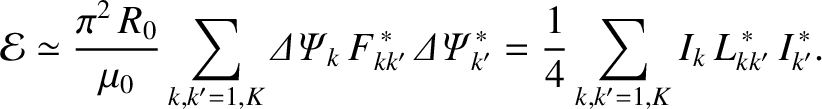 |
(14.99) |
 is a manifestly real quantity. Hence, it follows from the previous equation that the inductance matrix,
is a manifestly real quantity. Hence, it follows from the previous equation that the inductance matrix,  , must be Hermitian, which implies that the
normalized inductance matrix,
, must be Hermitian, which implies that the
normalized inductance matrix, 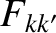 , is also Hermitian: that is,
, is also Hermitian: that is,
There is another reason why the F-matrix, 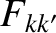 , must be Hermitian. According to Equation (14.70) and (14.94), the net toroidal electromagnetic torque
acting on the plasma is
, must be Hermitian. According to Equation (14.70) and (14.94), the net toroidal electromagnetic torque
acting on the plasma is
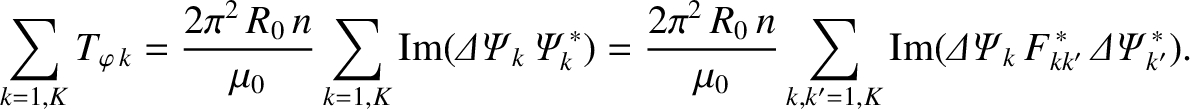 |
(14.101) |