Next: Bibliography Up: Neoclassical Theory Previous: Neoclassical Fluid Velocities Contents
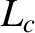 , that appears in the Rutherford island width evolution
equation, (12.15).
Let
, that appears in the Rutherford island width evolution
equation, (12.15).
Let
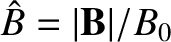 ,
,
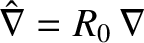 , and
, and
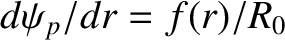 .
Furthermore, let
.
Furthermore, let
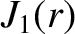 |
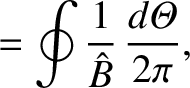 |
(A.89) |
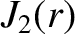 |
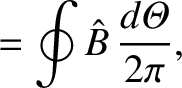 |
(A.90) |
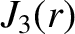 |
 |
(A.91) |
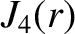 |
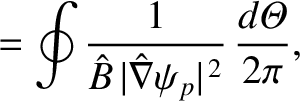 |
(A.92) |
 |
 |
(A.93) |
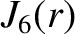 |
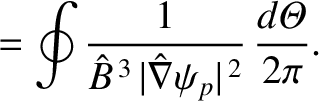 |
(A.94) |
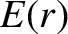 |
![$\displaystyle = - \frac{dP/d\psi_p}{(dq/d\psi_p)^{2}}\,\frac{1}{\gamma}\left[\f...
...t(\frac{J_1}{\gamma}\right) - g\,\frac{dq}{d\psi_p}\,\frac{J_1}{J_2}\right]J_5,$](img4868.png) |
(A.95) |
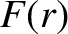 |
![$\displaystyle = \frac{(dP/d\psi_p)^{\,2}}{(dq/d\psi_p)^{2}}\,\frac{1}{\gamma^{2}}\left[g^{2}\left(J_5\,J_6- J_4^{\,2}\right)+ J_5\,J_3\right],$](img4869.png) |
(A.96) |
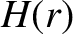 |
 |
(A.97) |
 , and
, and 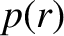 is the equilibrium plasma pressure.
Finally,
The value of the dimensionless parameter
is the equilibrium plasma pressure.
Finally,
The value of the dimensionless parameter 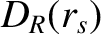 at a given rational magnetic flux-surface is related to the magnetic curvature length,
at a given rational magnetic flux-surface is related to the magnetic curvature length, 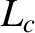 , introduced in Section 11.4, according to
Here,
, introduced in Section 11.4, according to
Here,
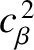 is a dimensionless measure of the plasma pressure at the rational surface [see Equations (4.65) and (4.66)],
is a dimensionless measure of the plasma pressure at the rational surface [see Equations (4.65) and (4.66)],
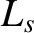 the magnetic shear-length at the rational surface [see Equation (5.27)], and
the magnetic shear-length at the rational surface [see Equation (5.27)], and  the effective pressure gradient scale-length at the rational surface [see Equation (8.35)]. The previous equation is a generalization of Equation (11.57).
The latter equation only holds in a large-aspect ratio, low-
the effective pressure gradient scale-length at the rational surface [see Equation (8.35)]. The previous equation is a generalization of Equation (11.57).
The latter equation only holds in a large-aspect ratio, low-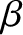 , tokamak plasma with magnetic flux-surfaces of circular cross-section.
, tokamak plasma with magnetic flux-surfaces of circular cross-section.