Next: Glasser-Greene-Johnson Parameters Up: Neoclassical Theory Previous: Parallel Force and Heat Contents
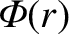 is the equilibrium electric scalar potential,
is the equilibrium electric scalar potential,
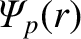 the equilibrium poloidal magnetic flux [see Equation (14.25)], and
the equilibrium poloidal magnetic flux [see Equation (14.25)], and
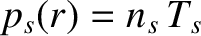 the species-
the species- pressure.
Note that
pressure.
Note that
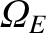 ,
,
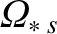 , and
, and
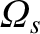 all have the dimensions of frequency.
Furthermore, let
Finally,
[See Equation (2.148).]
all have the dimensions of frequency.
Furthermore, let
Finally,
[See Equation (2.148).]
As is described in Reference [7], and is illustrated in a simplified form in Sections 2.14–2.20, we can determine the equilibrium fluid velocities of the various species that make up the plasma by balancing the parallel viscous force density against the parallel friction force density and the force density due to the parallel component of the electric field. We obtain [2,3,4,5]:
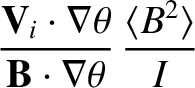 |
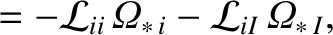 |
(A.83) |
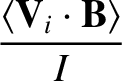 |
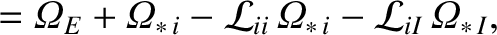 |
(A.84) |
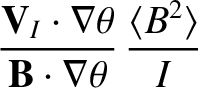 |
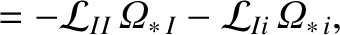 |
(A.85) |
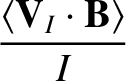 |
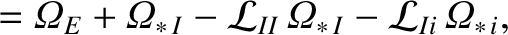 |
(A.86) |
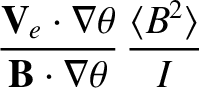 |
 |
(A.87) |
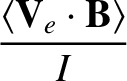 |
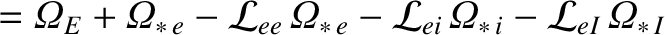 |
|
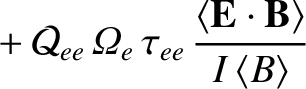 |
(A.88) |
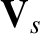 is the species-
is the species- equilibrium fluid velocity. The previous equations are generalizations of Equations (2.219), (2.221), (2.255), and (2.257).
The additional effects included in the generalized equations are a frictional drag due to impurities ions, a fraction of trapped particles that is not necessarily small, and
a plasma collisionality that is not necessarily in the banana regime.
equilibrium fluid velocity. The previous equations are generalizations of Equations (2.219), (2.221), (2.255), and (2.257).
The additional effects included in the generalized equations are a frictional drag due to impurities ions, a fraction of trapped particles that is not necessarily small, and
a plasma collisionality that is not necessarily in the banana regime.