Parallel Force and Heat Balance

Let

$$[\tilde{\mu}_{I}] =\alpha_I^{\,2}\,\frac{T_i}{T_I}\,x_{Ii}\,[\mu_{I}].$$ (A.69)

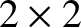The requirement of equilibrium force and heat balance parallel to the magnetic field (see Sections 2.18 and 2.19) leads us to define four $2\times 2$ dimensionless ion matrices, $[L_{ii}](r)$, $[L_{iI}](r)$, $[L_{Ii}](r)$, and $[L_{II}](r)$, where [7,9]

$$\left(\begin{array}{cc} [L_{ii}], & [L_{iI}]\\ [0.5ex] [L_{Ii}],&... ...y}{cc} [F_{ii}], & -[F_{iI}]\\ [0.5ex] -[F_{Ii}], & [F_{II}]\end{array}\right),$$ (A.70)

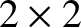and the $2\times 2$ dimensionless electron matrices, $[Q_{ee}](r)$, $[L_{ee}](r)$, $[L_{ei}](r)$, and $[L_{\,eI}](r)$, where

$$[Q_{ee}] = [F_{ee}+\mu_{e}]^{\,-1},$$ (A.71)

$$[L_{ee}] = [Q_{ee}]\,[F_{ee}],$$ (A.72)

$$[L_{ei}] = [Q_{ee}]\left\{[F_{ei}\,]\,[L_{ii}]-[F_{ei}]+[F_{eI}]\,[L_{Ii}]\right\},$$ (A.73)

$$[L_{eI}] = [Q_{ee}]\left\{[F_{eI}]\,[L_{II}]-[F_{eI}]+[F_{ei}]\,[L_{iI}]\right\}.$$ (A.74)