Next: Parallel Force and Heat Up: Neoclassical Theory Previous: Friction Force Matrices Contents
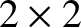 dimensionless species-
dimensionless species-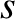 neoclassical viscosity matrix,
neoclassical viscosity matrix,
$](img4771.png) (see Section 2.17), is defined to have the following elements [7]:
(see Section 2.17), is defined to have the following elements [7]:
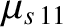 |
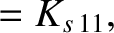 |
(A.53) |
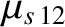 |
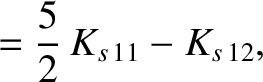 |
(A.54) |
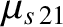 |
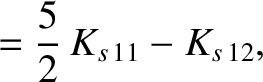 |
(A.55) |
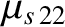 |
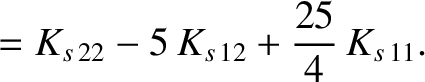 |
(A.56) |
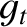 .)
Here,
and
.)
Here,
and
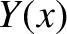 |
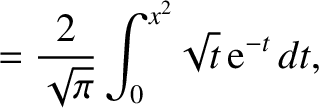 |
(A.61) |
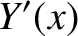 |
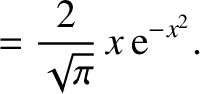 |
(A.62) |