Next: Neoclassical Viscosity Matrices Up: Neoclassical Theory Previous: Collisionality Parameters Contents
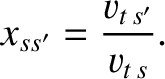 |
(A.24) |
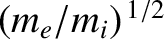 ,
,
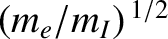 , or smaller, are neglected with respect to unity.
The
, or smaller, are neglected with respect to unity.
The  dimensionless ion collisional friction force matrices,
dimensionless ion collisional friction force matrices,
$](img4723.png) ,
,
$](img4724.png) ,
,
$](img4725.png) , and
, and
$](img4726.png) , are defined to have the following elements (see Section 2.16) [7,9]:
, are defined to have the following elements (see Section 2.16) [7,9]:
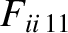 |
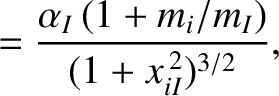 |
(A.25) |
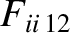 |
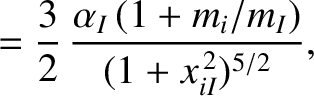 |
(A.26) |
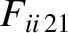 |
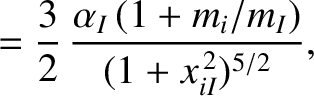 |
(A.27) |
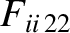 |
![$\displaystyle =\sqrt{2}+ \frac{\alpha_I\,[13/4+4\,x_{iI}^{\,2}+(15/2)\,x_{iI}^{\,4}]}{(1+x_{iI}^{\,2})^{5/2}},$](img4733.png) |
(A.28) |
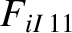 |
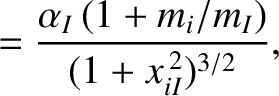 |
(A.29) |
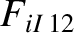 |
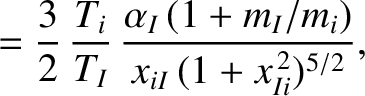 |
(A.30) |
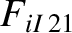 |
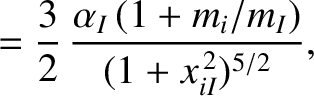 |
(A.31) |
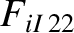 |
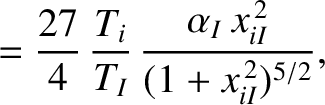 |
(A.32) |
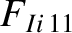 |
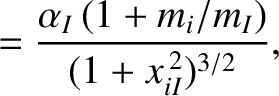 |
(A.33) |
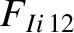 |
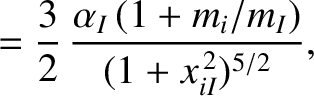 |
(A.34) |
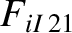 |
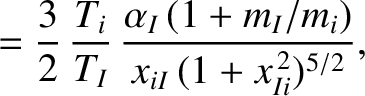 |
(A.35) |
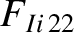 |
 |
(A.36) |
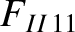 |
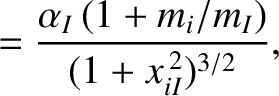 |
(A.37) |
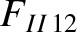 |
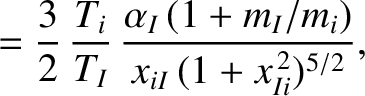 |
(A.38) |
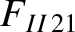 |
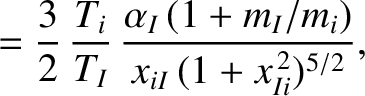 |
(A.39) |
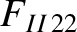 |
![$\displaystyle =\frac{T_i}{T_I}\left\{\sqrt{2}\,\alpha_I^{\,2}\,x_{Ii} + \frac{\...
...,[
15/2+4\,x_{iI}^{\,2}+(13/4)\,x_{iI}^{\,4}]}{(1+x_{iI}^{\,2})^{5/2}}\right\}.$](img4748.png) |
(A.40) |
The  dimensionless electron collisional friction force matrices,
dimensionless electron collisional friction force matrices,
$](img4749.png) ,
,
$](img4750.png) , and
, and
![$F_{eI}(r)]$](img4751.png) are defined to have the following elements (see Section 2.16) [7,9]:
are defined to have the following elements (see Section 2.16) [7,9]:
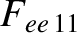 |
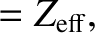 |
(A.41) |
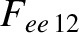 |
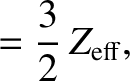 |
(A.42) |
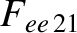 |
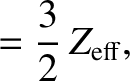 |
(A.43) |
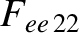 |
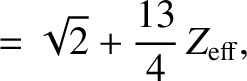 |
(A.44) |
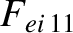 |
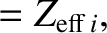 |
(A.45) |
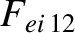 |
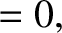 |
(A.46) |
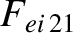 |
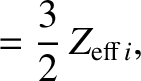 |
(A.47) |
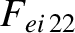 |
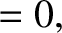 |
(A.48) |
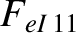 |
 |
(A.49) |
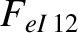 |
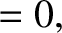 |
(A.50) |
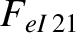 |
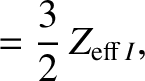 |
(A.51) |
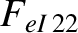 |
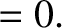 |
(A.52) |