Transformation of Electromagnetic Fields
In this section, we shall investigate how electromagnetic fields transform when viewed in different inertial
frames of reference. Our investigation is premised on two assumptions. First, Maxwell's equations (see Section 2.4.2) take equivalent forms in all
inertial frames of reference. Of course, this is
just a special case of the equivalence principle discussed in Section 3.2.1. Second, the electric charge of an elementary particle is the same in all inertial reference frames. Our second assumption is an experimentally verifiable fact.
Figure 3.16:
Parallel plate capacitor.
|
|
Consider three inertial reference frames, 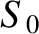 ,
,  , and
, and  , that are all in standard configurations with respect to
one another. (See Section 3.2.6.) Let frame
, that are all in standard configurations with respect to
one another. (See Section 3.2.6.) Let frame  move parallel to the
move parallel to the  -axis at speed
-axis at speed 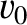 with respect to frame
with respect to frame 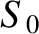 . Let
frame
. Let
frame  move parallel to the
move parallel to the  -axis at speed
-axis at speed 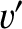 with respect to frame
with respect to frame 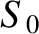 , and with speed
, and with speed  with respect to
frame
with respect to
frame  . See Figure 3.16. It follows from the relativistic transformation of velocity (see Section 3.2.9) that
. See Figure 3.16. It follows from the relativistic transformation of velocity (see Section 3.2.9) that
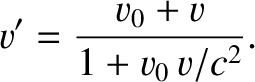 |
(3.249) |
Let us define the Lorentz factors
The previous four equations yield
Suppose that frame 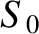 contains a parallel plate capacitor that is at rest. Let the capacitor
plates be parallel to the
contains a parallel plate capacitor that is at rest. Let the capacitor
plates be parallel to the  -
- plane. Furthermore, let the lower (in
plane. Furthermore, let the lower (in  ) plate have the uniform electric charge
density
) plate have the uniform electric charge
density  , and let the upper plate have the uniform charge density
, and let the upper plate have the uniform charge density 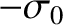 . See Figure 3.16.
In frame
. See Figure 3.16.
In frame  , the capacitor plates appear to move in the
, the capacitor plates appear to move in the 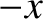 -direction with speed
-direction with speed 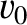 . Thus, the lengths
of the plates (in the
. Thus, the lengths
of the plates (in the  -direction) are contracted by a factor
-direction) are contracted by a factor 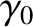 , whereas the widths of the plates (in the
, whereas the widths of the plates (in the
 -direction) are unchanged. (See Section 3.2.7.) Moreover, according to
our second assumption, the net electric
charges on the two capacitor plates in frame
-direction) are unchanged. (See Section 3.2.7.) Moreover, according to
our second assumption, the net electric
charges on the two capacitor plates in frame  are the same as those in frame
are the same as those in frame 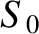 . It follows that, in frame
. It follows that, in frame  , the charge densities on the two plates are
, the charge densities on the two plates are  , where
, where
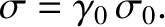 |
(3.254) |
Analogous reasoning reveals that the charge densities on the two capacitor plates in frame  are
are
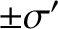 , where
, where
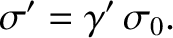 |
(3.255) |
All of the electric charges in frame 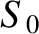 are stationary, so the associated current density is zero. However, in frames
are stationary, so the associated current density is zero. However, in frames
 and
and  , the
charges on the capacitor plates appear to move in the
, the
charges on the capacitor plates appear to move in the 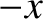 -direction with speeds
-direction with speeds 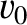 and
and 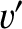 , respectively. Thus, in frame
, respectively. Thus, in frame  , the current per unit width (in the
, the current per unit width (in the  -direction) flowing on the lower (in
-direction) flowing on the lower (in  ) capacitor plate takes the
form
) capacitor plate takes the
form
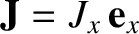 , where
, where
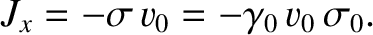 |
(3.256) |
There is an equal and opposite current per unit width flowing on the upper plate. Likewise, in frame  , the current per unit width flowing on the lower plate takes the form
, the current per unit width flowing on the lower plate takes the form
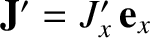 , where
, where
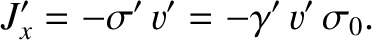 |
(3.257) |
Again, there is an equal and opposite current per unit width flowing on the upper plate.
The integral form of the Maxwell equation (2.484) is
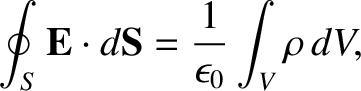 |
(3.258) |
where  is some surface enclosing a volume
is some surface enclosing a volume  , and
where use has been made of the divergence theorem. (See Section A.20.) As described in Sections 2.1.12 and 2.1.13, if the previous equation is
applied to a Gaussian pill-box in frame
, and
where use has been made of the divergence theorem. (See Section A.20.) As described in Sections 2.1.12 and 2.1.13, if the previous equation is
applied to a Gaussian pill-box in frame  that encloses one or other of the capacitor plates, and co-moves with the plates, then it
is easily demonstrated that the electric field in the region between the plates is uniform, taking the
form
that encloses one or other of the capacitor plates, and co-moves with the plates, then it
is easily demonstrated that the electric field in the region between the plates is uniform, taking the
form
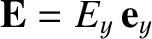 , where
, where
 |
(3.259) |
Note, incidentally, that there is nothing in Equation (3.258) that precludes volume  from being
a moving volume. Analogous reasoning reveals that the electric field between the capacitor plates in frame
from being
a moving volume. Analogous reasoning reveals that the electric field between the capacitor plates in frame
 is uniform, taking the value
is uniform, taking the value
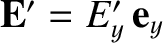 , where
, where
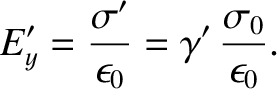 |
(3.260) |
The integral form of the Maxwell equation (2.487) is
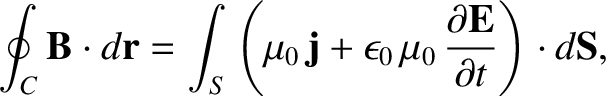 |
(3.261) |
where  is a surface bounded by a loop
is a surface bounded by a loop  , and where use has been made of the curl theorem. (See Section A.22.) However, the electric field between the capacitor plates is constant in time in all
three of our reference frames, so the previous equation simplifies to give
, and where use has been made of the curl theorem. (See Section A.22.) However, the electric field between the capacitor plates is constant in time in all
three of our reference frames, so the previous equation simplifies to give
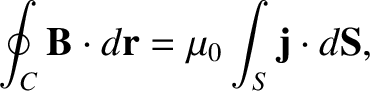 |
(3.262) |
If the previous equation is applied to an Ampèrian loop in the  -
- plane of frame
plane of frame  that straddles one or other of the capacitor plates, and
co-moves with the plates, then it is easily demonstrated that the magnetic field in the region between
the plates is uniform, taking the form
that straddles one or other of the capacitor plates, and
co-moves with the plates, then it is easily demonstrated that the magnetic field in the region between
the plates is uniform, taking the form
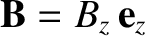 , where
, where
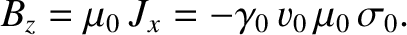 |
(3.263) |
Again, there is nothing in Equation (3.262) that prohibits surface  from being a moving
surface. Likewise, in frame
from being a moving
surface. Likewise, in frame  , the magnetic field between the plates is uniform,
taking the form
, the magnetic field between the plates is uniform,
taking the form
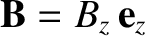 , where
, where
 |
(3.264) |
According to Equations (3.253), (3.259), (3.260), and (3.263),
where use has been made of
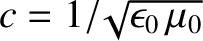 . Likewise, Equation (3.249), (3.253),
(3.259), (3.263), and (3.264) yield
. Likewise, Equation (3.249), (3.253),
(3.259), (3.263), and (3.264) yield
If we repeat the previous exercise with capacitor plates that are parallel to the  -
- plane, instead of the
plane, instead of the
 -
- plane, then it is easily demonstrated that
plane, then it is easily demonstrated that
Figure 3.17:
Parallel plate capacitor.
|
|
In order to determine the transformation rule for 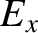 , consider the situation shown in Figure 3.17.
Here, a parallel plate capacitor is stationary in frame
, consider the situation shown in Figure 3.17.
Here, a parallel plate capacitor is stationary in frame  , and is aligned such that its plates are parallel to the
, and is aligned such that its plates are parallel to the  -
- plane. Frame
plane. Frame  is in a standard configuration, and moves with velocity
is in a standard configuration, and moves with velocity
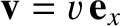 , with respect to frame
, with respect to frame  .
The cross-sectional areas of the plates are the same in reference frames
.
The cross-sectional areas of the plates are the same in reference frames  and
and  . (See Section 3.2.7.) Furthermore, the
electric charges on the plates are identical in both frames. Hence, we deduce that the electric charge densities on the plates are
the same in the two reference frames. In other words,
. (See Section 3.2.7.) Furthermore, the
electric charges on the plates are identical in both frames. Hence, we deduce that the electric charge densities on the plates are
the same in the two reference frames. In other words,
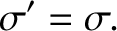 |
(3.269) |
Now, the
parallel distance between the two plates is contracted by a factor  in frame
in frame  , compared to
frame
, compared to
frame  . However, the electric field generated between the capacitor plates only depends on the charge
density residing on the plates, and is independent of the inter-plate spacing. In fact, the electric fields in
frames
. However, the electric field generated between the capacitor plates only depends on the charge
density residing on the plates, and is independent of the inter-plate spacing. In fact, the electric fields in
frames  and
and  are
are
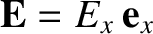 and
and
 , respectively,
where
Hence, we deduce from the previous three equations that
, respectively,
where
Hence, we deduce from the previous three equations that
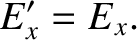 |
(3.272) |
In order to determine the transformation for 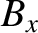 , consider a long, thin, solenoid whose axis runs parallel to the
, consider a long, thin, solenoid whose axis runs parallel to the
 -direction. Let the solenoid have
-direction. Let the solenoid have  turns per unit length, and carry a current
turns per unit length, and carry a current  , in frame
, in frame  , and
let the solenoid have
, and
let the solenoid have 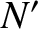 turns per unit length, and carry a current
turns per unit length, and carry a current 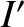 , in frame
, in frame  . Frame
. Frame  is in a standard configuration, and moves with velocity
is in a standard configuration, and moves with velocity
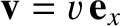 , with respect to frame
, with respect to frame  .
Because of relativistic length contraction (see Section 3.2.4),
.
Because of relativistic length contraction (see Section 3.2.4),
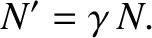 |
(3.273) |
On the other hand, because current is electric charge per unit time, and electric charge is invariant between different inertial
frames, whereas time is dilated in frame  , relative to frame
, relative to frame  , we have
, we have
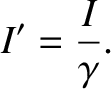 |
(3.274) |
According to Section 2.2.11, the magnetic fields generated inside the solenoid in frames  and
and  are
are
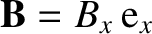 and
and
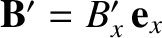 , respectively, where
The previous four equations imply that
, respectively, where
The previous four equations imply that
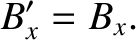 |
(3.277) |
Thus, we can now state the complete set of transformation laws for the components of the electric and magnetic field
between an inertial reference frame  , and a second inertial reference frame,
, and a second inertial reference frame,  , that is in a standard configuration, and moves at velocity
, that is in a standard configuration, and moves at velocity
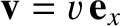 , with respect to the first.
The transformation laws are as follows:
, with respect to the first.
The transformation laws are as follows:
and
Here,
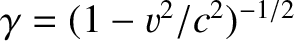 .
.
It is easily demonstrated from the transformation rules (3.278)–(3.283) that
Thus, if electric and magnetic fields in one inertial frame of reference are in the
configuration of an electromagnetic wave traveling through a vacuum—in other words, if
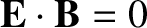 and
and 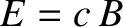 (see Section 2.4.4)—then they are in this configuration in
all inertial frames of reference.
(see Section 2.4.4)—then they are in this configuration in
all inertial frames of reference.
 ,
,  , and
, and  , that are all in standard configurations with respect to
one another. (See Section 3.2.6.) Let frame
, that are all in standard configurations with respect to
one another. (See Section 3.2.6.) Let frame  move parallel to the
move parallel to the  -axis at speed
-axis at speed 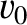 with respect to frame
with respect to frame 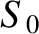 . Let
frame
. Let
frame  move parallel to the
move parallel to the  -axis at speed
-axis at speed 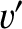 with respect to frame
with respect to frame 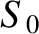 , and with speed
, and with speed  with respect to
frame
with respect to
frame  . See Figure 3.16. It follows from the relativistic transformation of velocity (see Section 3.2.9) that
. See Figure 3.16. It follows from the relativistic transformation of velocity (see Section 3.2.9) that
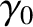
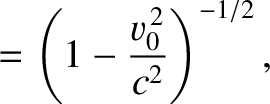
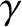

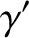
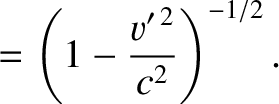
 contains a parallel plate capacitor that is at rest. Let the capacitor
plates be parallel to the
contains a parallel plate capacitor that is at rest. Let the capacitor
plates be parallel to the  -
- plane. Furthermore, let the lower (in
plane. Furthermore, let the lower (in  ) plate have the uniform electric charge
density
) plate have the uniform electric charge
density  , and let the upper plate have the uniform charge density
, and let the upper plate have the uniform charge density  . See Figure 3.16.
In frame
. See Figure 3.16.
In frame  , the capacitor plates appear to move in the
, the capacitor plates appear to move in the  -direction with speed
-direction with speed 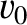 . Thus, the lengths
of the plates (in the
. Thus, the lengths
of the plates (in the  -direction) are contracted by a factor
-direction) are contracted by a factor 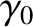 , whereas the widths of the plates (in the
, whereas the widths of the plates (in the
 -direction) are unchanged. (See Section 3.2.7.) Moreover, according to
our second assumption, the net electric
charges on the two capacitor plates in frame
-direction) are unchanged. (See Section 3.2.7.) Moreover, according to
our second assumption, the net electric
charges on the two capacitor plates in frame  are the same as those in frame
are the same as those in frame 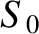 . It follows that, in frame
. It follows that, in frame  , the charge densities on the two plates are
, the charge densities on the two plates are  , where
, where
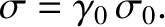
 are
are
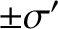 , where
, where
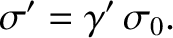
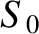 are stationary, so the associated current density is zero. However, in frames
are stationary, so the associated current density is zero. However, in frames
 and
and  , the
charges on the capacitor plates appear to move in the
, the
charges on the capacitor plates appear to move in the 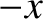 -direction with speeds
-direction with speeds 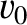 and
and 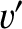 , respectively. Thus, in frame
, respectively. Thus, in frame  , the current per unit width (in the
, the current per unit width (in the  -direction) flowing on the lower (in
-direction) flowing on the lower (in  ) capacitor plate takes the
form
) capacitor plate takes the
form
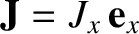 , where
, where
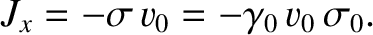
 , the current per unit width flowing on the lower plate takes the form
, the current per unit width flowing on the lower plate takes the form
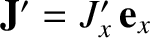 , where
, where
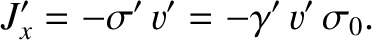
 is some surface enclosing a volume
is some surface enclosing a volume  , and
where use has been made of the divergence theorem. (See Section A.20.) As described in Sections 2.1.12 and 2.1.13, if the previous equation is
applied to a Gaussian pill-box in frame
, and
where use has been made of the divergence theorem. (See Section A.20.) As described in Sections 2.1.12 and 2.1.13, if the previous equation is
applied to a Gaussian pill-box in frame  that encloses one or other of the capacitor plates, and co-moves with the plates, then it
is easily demonstrated that the electric field in the region between the plates is uniform, taking the
form
that encloses one or other of the capacitor plates, and co-moves with the plates, then it
is easily demonstrated that the electric field in the region between the plates is uniform, taking the
form
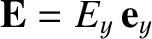 , where
Note, incidentally, that there is nothing in Equation (3.258) that precludes volume
, where
Note, incidentally, that there is nothing in Equation (3.258) that precludes volume  from being
a moving volume. Analogous reasoning reveals that the electric field between the capacitor plates in frame
from being
a moving volume. Analogous reasoning reveals that the electric field between the capacitor plates in frame
 is uniform, taking the value
is uniform, taking the value
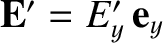 , where
, where
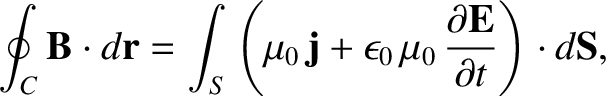
 is a surface bounded by a loop
is a surface bounded by a loop  , and where use has been made of the curl theorem. (See Section A.22.) However, the electric field between the capacitor plates is constant in time in all
three of our reference frames, so the previous equation simplifies to give
, and where use has been made of the curl theorem. (See Section A.22.) However, the electric field between the capacitor plates is constant in time in all
three of our reference frames, so the previous equation simplifies to give
 -
- plane of frame
plane of frame  that straddles one or other of the capacitor plates, and
co-moves with the plates, then it is easily demonstrated that the magnetic field in the region between
the plates is uniform, taking the form
that straddles one or other of the capacitor plates, and
co-moves with the plates, then it is easily demonstrated that the magnetic field in the region between
the plates is uniform, taking the form
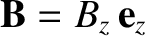 , where
, where
 from being a moving
surface. Likewise, in frame
from being a moving
surface. Likewise, in frame  , the magnetic field between the plates is uniform,
taking the form
, the magnetic field between the plates is uniform,
taking the form
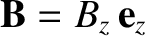 , where
, where

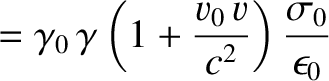

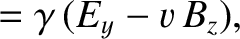
 . Likewise, Equation (3.249), (3.253),
(3.259), (3.263), and (3.264) yield
. Likewise, Equation (3.249), (3.253),
(3.259), (3.263), and (3.264) yield

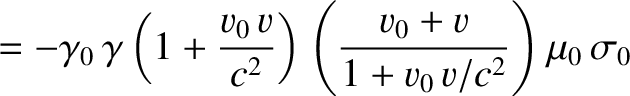
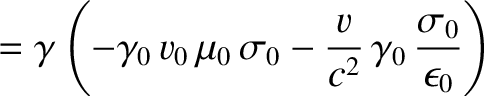
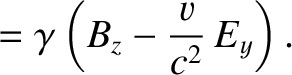
 -
- plane, instead of the
plane, instead of the
 -
- plane, then it is easily demonstrated that
plane, then it is easily demonstrated that
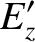
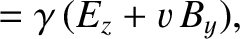
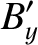

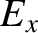 , consider the situation shown in Figure 3.17.
Here, a parallel plate capacitor is stationary in frame
, consider the situation shown in Figure 3.17.
Here, a parallel plate capacitor is stationary in frame  , and is aligned such that its plates are parallel to the
, and is aligned such that its plates are parallel to the  -
- plane. Frame
plane. Frame  is in a standard configuration, and moves with velocity
is in a standard configuration, and moves with velocity
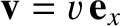 , with respect to frame
, with respect to frame  .
The cross-sectional areas of the plates are the same in reference frames
.
The cross-sectional areas of the plates are the same in reference frames  and
and  . (See Section 3.2.7.) Furthermore, the
electric charges on the plates are identical in both frames. Hence, we deduce that the electric charge densities on the plates are
the same in the two reference frames. In other words,
. (See Section 3.2.7.) Furthermore, the
electric charges on the plates are identical in both frames. Hence, we deduce that the electric charge densities on the plates are
the same in the two reference frames. In other words,
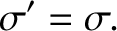
 in frame
in frame  , compared to
frame
, compared to
frame  . However, the electric field generated between the capacitor plates only depends on the charge
density residing on the plates, and is independent of the inter-plate spacing. In fact, the electric fields in
frames
. However, the electric field generated between the capacitor plates only depends on the charge
density residing on the plates, and is independent of the inter-plate spacing. In fact, the electric fields in
frames  and
and  are
are
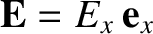 and
and
 , respectively,
where
, respectively,
where
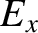
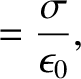
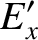
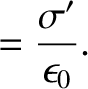
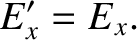
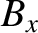 , consider a long, thin, solenoid whose axis runs parallel to the
, consider a long, thin, solenoid whose axis runs parallel to the
 -direction. Let the solenoid have
-direction. Let the solenoid have  turns per unit length, and carry a current
turns per unit length, and carry a current  , in frame
, in frame  , and
let the solenoid have
, and
let the solenoid have 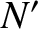 turns per unit length, and carry a current
turns per unit length, and carry a current 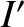 , in frame
, in frame  . Frame
. Frame  is in a standard configuration, and moves with velocity
is in a standard configuration, and moves with velocity
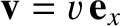 , with respect to frame
, with respect to frame  .
Because of relativistic length contraction (see Section 3.2.4),
.
Because of relativistic length contraction (see Section 3.2.4),
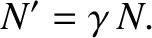
 , relative to frame
, relative to frame  , we have
, we have
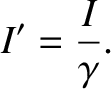
 and
and  are
are
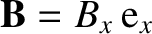 and
and
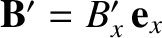 , respectively, where
, respectively, where
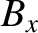
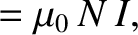
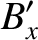
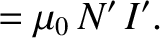
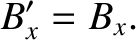
 , and a second inertial reference frame,
, and a second inertial reference frame,  , that is in a standard configuration, and moves at velocity
, that is in a standard configuration, and moves at velocity
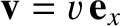 , with respect to the first.
The transformation laws are as follows:
, with respect to the first.
The transformation laws are as follows:
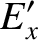
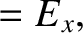

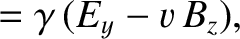
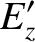
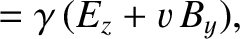
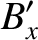
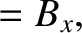
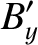
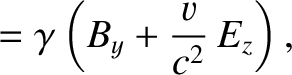

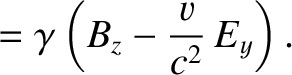
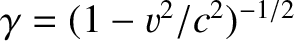 .
.

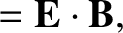
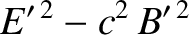

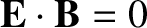 and
and 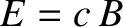 (see Section 2.4.4)—then they are in this configuration in
all inertial frames of reference.
(see Section 2.4.4)—then they are in this configuration in
all inertial frames of reference.