Next: Lorentz Transformation Up: Theoretical Basis of Special Previous: Clock Error
Consider two inertial frames of reference,  and
and  . Let frame
. Let frame  move at velocity
move at velocity  with respect to
frame
with respect to
frame  . Let us set up right-handed Cartesian coordinate systems in both frames. Suppose that the coordinate systems are
in the so-called standard configuration in which the corresponding coordinate axes are parallel, the
. Let us set up right-handed Cartesian coordinate systems in both frames. Suppose that the coordinate systems are
in the so-called standard configuration in which the corresponding coordinate axes are parallel, the  -axis in each system is
parallel to
-axis in each system is
parallel to  , and the origins of the systems coincide at time
, and the origins of the systems coincide at time  . See Figure 3.9. Consider an instantaneous `event' with a definite
spatial location, such as the flashing of a light-bulb. Suppose that the event occurs at time
. See Figure 3.9. Consider an instantaneous `event' with a definite
spatial location, such as the flashing of a light-bulb. Suppose that the event occurs at time  and has displacement (
and has displacement ( ,
,  ,
,  ) in frame
) in frame  . Suppose that the event occurs at time
. Suppose that the event occurs at time 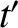 and has displacement (
and has displacement (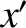 ,
, 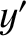 ,
, 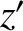 ) in frame
) in frame  . What is the relationship between (
. What is the relationship between ( ,
,  ,
,  ,
,  ) and (
) and (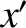 ,
, 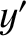 ,
, 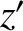 ,
, 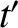 ). Well, according to standard Newtonian
physics, the “common sense” relationship between the two sets of coordinates is
). Well, according to standard Newtonian
physics, the “common sense” relationship between the two sets of coordinates is
 are
are 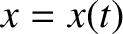 ,
, 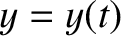 , and
, and  . The Cartesian components of the instantaneous velocity of our
event in
. The Cartesian components of the instantaneous velocity of our
event in  are
are  ,
, 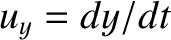 ,
,  , whereas the corresponding components in
, whereas the corresponding components in
 are
are
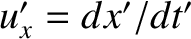 ,
,
 ,
,
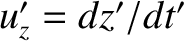 . Hence, we can derive the following Galilean velocity
transformation from Equations (3.88)–(3.91):
. Hence, we can derive the following Galilean velocity
transformation from Equations (3.88)–(3.91):
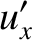 |
 |
(3.92) |
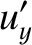 |
 |
(3.93) |
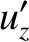 |
 |
(3.94) |
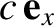 in
in  then, according
to the Galilean velocity transform, the light ray moves with velocity
then, according
to the Galilean velocity transform, the light ray moves with velocity
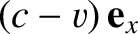 in
in  . In other words, the
light ray travels at difference speeds in the two frames of reference. However, this state of affairs is forbidden by Einstein's
first postulate. Hence, we deduce that the Galilean transformation, (3.88)–(3.91), is actually inconsistent with the theory of relativity.
. In other words, the
light ray travels at difference speeds in the two frames of reference. However, this state of affairs is forbidden by Einstein's
first postulate. Hence, we deduce that the Galilean transformation, (3.88)–(3.91), is actually inconsistent with the theory of relativity.