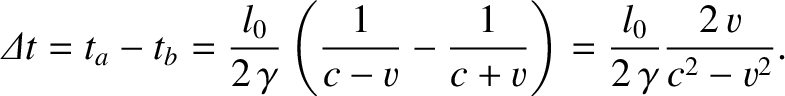Consider two clocks,  and
and  , that are located a distance
, that are located a distance 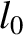 apart in their mutual rest frame. Suppose that the
clocks are synchronized using light pulses emitted from a source that lies half-way between them.
Let us observe the clocks in a reference frame that moves with velocity
apart in their mutual rest frame. Suppose that the
clocks are synchronized using light pulses emitted from a source that lies half-way between them.
Let us observe the clocks in a reference frame that moves with velocity  with respect to the clocks'
rest frame in a direction that is parallel to their mutual displacement. See Figure 3.8. In the moving frame, the
contracted distance between the two clocks is
with respect to the clocks'
rest frame in a direction that is parallel to their mutual displacement. See Figure 3.8. In the moving frame, the
contracted distance between the two clocks is
 , but the source is still located half-way between the clocks. Moreover, the two clocks appear to move with the same velocity,
, but the source is still located half-way between the clocks. Moreover, the two clocks appear to move with the same velocity, 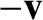 . Consider a light pulse that is
emitted by the source and travels to the two clocks. Suppose that, in the moving frame, it takes a time
. Consider a light pulse that is
emitted by the source and travels to the two clocks. Suppose that, in the moving frame, it takes a time 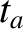 for the pulse to travel from the
source to clock
for the pulse to travel from the
source to clock  . The pulse travels a distance
. The pulse travels a distance
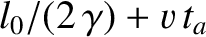 . Thus, given that the pulse travels at the
speed
. Thus, given that the pulse travels at the
speed  , according to Einstein's second postulate, we have
, according to Einstein's second postulate, we have
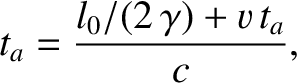 |
(3.82) |
or
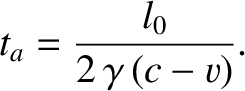 |
(3.83) |
Suppose that, in the moving frame, it takes a time 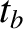 for the pulse to travel from the source to clock
for the pulse to travel from the source to clock  .
The pulse travels a distance
.
The pulse travels a distance
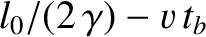 . Thus, given that the pulse travels at the
speed
. Thus, given that the pulse travels at the
speed  , we have
, we have
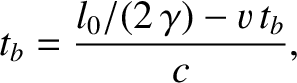 |
(3.84) |
or
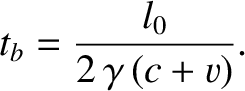 |
(3.85) |
Now, in the clocks' rest frame, the pulse arrives at clocks  and
and  simultaneously. However, in the moving
frame, the pulse arrives at clock
simultaneously. However, in the moving
frame, the pulse arrives at clock  prior to its arrival at clock
prior to its arrival at clock  (because
(because 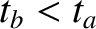 ).
In other words, two events, a spatial distance
).
In other words, two events, a spatial distance 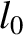 apart,
that take place simultaneously in a particular reference frame, do not appear to take place simultaneously
in a reference frame that moves with velocity
apart,
that take place simultaneously in a particular reference frame, do not appear to take place simultaneously
in a reference frame that moves with velocity  in the direction of the mutual displacement of the two
events. This phenomenon is known as clock error. The time difference between the two events in the
moving frame is
in the direction of the mutual displacement of the two
events. This phenomenon is known as clock error. The time difference between the two events in the
moving frame is
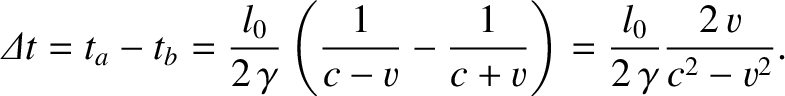 |
(3.86) |
which reduces to
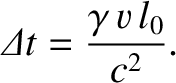 |
(3.87) |
 and
and  , that are located a distance
, that are located a distance 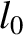 apart in their mutual rest frame. Suppose that the
clocks are synchronized using light pulses emitted from a source that lies half-way between them.
Let us observe the clocks in a reference frame that moves with velocity
apart in their mutual rest frame. Suppose that the
clocks are synchronized using light pulses emitted from a source that lies half-way between them.
Let us observe the clocks in a reference frame that moves with velocity  with respect to the clocks'
rest frame in a direction that is parallel to their mutual displacement. See Figure 3.8. In the moving frame, the
contracted distance between the two clocks is
with respect to the clocks'
rest frame in a direction that is parallel to their mutual displacement. See Figure 3.8. In the moving frame, the
contracted distance between the two clocks is
 , but the source is still located half-way between the clocks. Moreover, the two clocks appear to move with the same velocity,
, but the source is still located half-way between the clocks. Moreover, the two clocks appear to move with the same velocity, 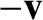 . Consider a light pulse that is
emitted by the source and travels to the two clocks. Suppose that, in the moving frame, it takes a time
. Consider a light pulse that is
emitted by the source and travels to the two clocks. Suppose that, in the moving frame, it takes a time 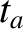 for the pulse to travel from the
source to clock
for the pulse to travel from the
source to clock  . The pulse travels a distance
. The pulse travels a distance
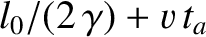 . Thus, given that the pulse travels at the
speed
. Thus, given that the pulse travels at the
speed  , according to Einstein's second postulate, we have
, according to Einstein's second postulate, we have
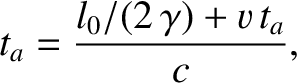
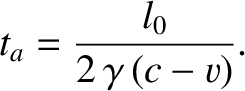
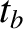 for the pulse to travel from the source to clock
for the pulse to travel from the source to clock  .
The pulse travels a distance
.
The pulse travels a distance
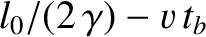 . Thus, given that the pulse travels at the
speed
. Thus, given that the pulse travels at the
speed  , we have
, we have
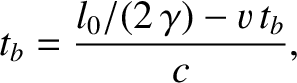
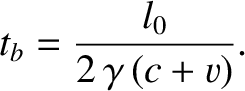
 and
and  simultaneously. However, in the moving
frame, the pulse arrives at clock
simultaneously. However, in the moving
frame, the pulse arrives at clock  prior to its arrival at clock
prior to its arrival at clock  (because
(because 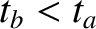 ).
In other words, two events, a spatial distance
).
In other words, two events, a spatial distance 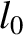 apart,
that take place simultaneously in a particular reference frame, do not appear to take place simultaneously
in a reference frame that moves with velocity
apart,
that take place simultaneously in a particular reference frame, do not appear to take place simultaneously
in a reference frame that moves with velocity  in the direction of the mutual displacement of the two
events. This phenomenon is known as clock error. The time difference between the two events in the
moving frame is
in the direction of the mutual displacement of the two
events. This phenomenon is known as clock error. The time difference between the two events in the
moving frame is