Length Contraction
Let us again consider the light-clock introduced in Section 3.2.3. As before, let 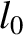 be the distance between the
clock and the reflector in the clock's rest frame. Thus, each tick of the clock in its rest frame corresponds to the time interval
be the distance between the
clock and the reflector in the clock's rest frame. Thus, each tick of the clock in its rest frame corresponds to the time interval
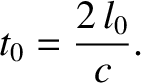 |
(3.74) |
[See Equation (3.66).]
Figure 3.7:
Length contraction.
|
|
Suppose that we observe the aforementioned clock in a frame of reference that moves with velocity  with respect
to the clock's rest frame, where the direction of
with respect
to the clock's rest frame, where the direction of  is parallel to the path of the light ray in the rest frame. See Figure 3.7. Let
is parallel to the path of the light ray in the rest frame. See Figure 3.7. Let  be the distance between the clock and the reflector in the moving frame.
In the moving frame, both the reflector and the clock appear to move at velocity
be the distance between the clock and the reflector in the moving frame.
In the moving frame, both the reflector and the clock appear to move at velocity 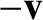 (because they are both at
rest in the clock's rest frame, and
(because they are both at
rest in the clock's rest frame, and 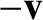 is the velocity of this frame relative to the moving frame).
Suppose that, in the moving frame, the light ray takes a time
is the velocity of this frame relative to the moving frame).
Suppose that, in the moving frame, the light ray takes a time 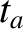 to travel from the clock to the reflector. The distance traveled by the
ray is
to travel from the clock to the reflector. The distance traveled by the
ray is
 . Hence, because the light ray travels at speed
. Hence, because the light ray travels at speed  in the moving frame (irrespective of the motion of
the clock or the reflector), according to Einstein's second postulate, we can write
in the moving frame (irrespective of the motion of
the clock or the reflector), according to Einstein's second postulate, we can write
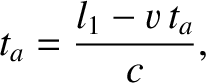 |
(3.75) |
which implies that
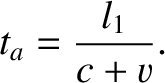 |
(3.76) |
Suppose that, in the moving frame, the light ray takes a time 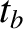 to travel from the reflector back to the clock. The distance traveled by the ray is
to travel from the reflector back to the clock. The distance traveled by the ray is 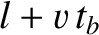 . Hence, we can write
. Hence, we can write
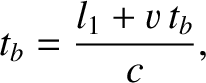 |
(3.77) |
which implies that
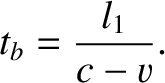 |
(3.78) |
The net time needed for the light ray to travel from the clock to the reflector, and back again, in the moving frame, is
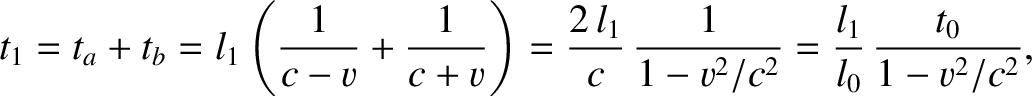 |
(3.79) |
where use has been made of Equation (3.74).
This time corresponds to the time interval of the clock's tick in the moving frame. However, we established in Section 3.2.3 that, as a consequence of time dilation,
 |
(3.80) |
Note that if our light clock does not suffer exactly the same time dilation as the clock in Section 3.2.3 then we
could distinguish between different inertial frames in terms of the different time dilations suffered by light-clocks
in which the light rays traveled parallel and perpendicular to the relative velocities of the frames. However, this
state of affairs is prohibited by Einstein's first postulate. The previous two equations yield
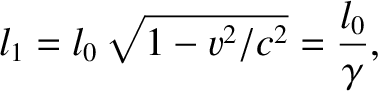 |
(3.81) |
where  is the Lorentz factor introduced in Equation (3.72).
In other words, the distance between the clock and the reflector appears
contracted by the Lorentz factor when viewed in the moving frame. Given that we could have placed the clock and the reflector at any two points in space, we conclude that a stationary and a moving observer will not agree on
measurements of lengths orientated parallel to their
relative motion. In fact, all such lengths will appear contracted by the Lorentz factor to the moving observer. This
effect is known as length contraction, and is equivalent to the Lorentz-Fitzgerald contraction discussed
in Section 3.1.6.
is the Lorentz factor introduced in Equation (3.72).
In other words, the distance between the clock and the reflector appears
contracted by the Lorentz factor when viewed in the moving frame. Given that we could have placed the clock and the reflector at any two points in space, we conclude that a stationary and a moving observer will not agree on
measurements of lengths orientated parallel to their
relative motion. In fact, all such lengths will appear contracted by the Lorentz factor to the moving observer. This
effect is known as length contraction, and is equivalent to the Lorentz-Fitzgerald contraction discussed
in Section 3.1.6.
Incidentally, we saw, in Sections 3.1.6 and 3.1.7, that length contraction alone is sufficient to explain the null result of the Michelson-Morley experiment, but not the Kennedy-Thorndike experiment. Hence, we conclude that both
length contraction and time dilation are needed to explain the null result of the Kennedy-Thorndike experiment.
Another way of saying this is that the null result of the Michelson-Morley experiment can be regarded as experimental
verification of length contraction, whereas the null result of the Kennedy-Thorndike experiment can be
regarded as experimental validation of time dilation. It should be noted that both of these experiments have
been repeated many times, over the years, and that the null results of the experiments are now established to very great accuracy.
 be the distance between the
clock and the reflector in the clock's rest frame. Thus, each tick of the clock in its rest frame corresponds to the time interval
[See Equation (3.66).]
be the distance between the
clock and the reflector in the clock's rest frame. Thus, each tick of the clock in its rest frame corresponds to the time interval
[See Equation (3.66).]
 with respect
to the clock's rest frame, where the direction of
with respect
to the clock's rest frame, where the direction of  is parallel to the path of the light ray in the rest frame. See Figure 3.7. Let
is parallel to the path of the light ray in the rest frame. See Figure 3.7. Let  be the distance between the clock and the reflector in the moving frame.
In the moving frame, both the reflector and the clock appear to move at velocity
be the distance between the clock and the reflector in the moving frame.
In the moving frame, both the reflector and the clock appear to move at velocity  (because they are both at
rest in the clock's rest frame, and
(because they are both at
rest in the clock's rest frame, and  is the velocity of this frame relative to the moving frame).
Suppose that, in the moving frame, the light ray takes a time
is the velocity of this frame relative to the moving frame).
Suppose that, in the moving frame, the light ray takes a time 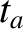 to travel from the clock to the reflector. The distance traveled by the
ray is
to travel from the clock to the reflector. The distance traveled by the
ray is
 . Hence, because the light ray travels at speed
. Hence, because the light ray travels at speed  in the moving frame (irrespective of the motion of
the clock or the reflector), according to Einstein's second postulate, we can write
in the moving frame (irrespective of the motion of
the clock or the reflector), according to Einstein's second postulate, we can write
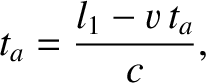
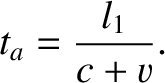
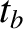 to travel from the reflector back to the clock. The distance traveled by the ray is
to travel from the reflector back to the clock. The distance traveled by the ray is 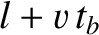 . Hence, we can write
. Hence, we can write
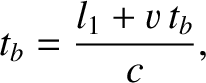
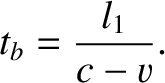
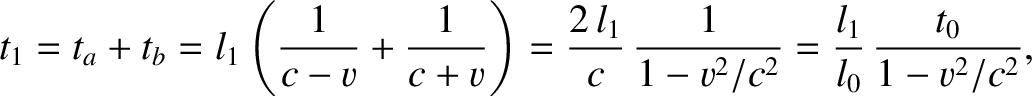

 is the Lorentz factor introduced in Equation (3.72).
In other words, the distance between the clock and the reflector appears
contracted by the Lorentz factor when viewed in the moving frame. Given that we could have placed the clock and the reflector at any two points in space, we conclude that a stationary and a moving observer will not agree on
measurements of lengths orientated parallel to their
relative motion. In fact, all such lengths will appear contracted by the Lorentz factor to the moving observer. This
effect is known as length contraction, and is equivalent to the Lorentz-Fitzgerald contraction discussed
in Section 3.1.6.
is the Lorentz factor introduced in Equation (3.72).
In other words, the distance between the clock and the reflector appears
contracted by the Lorentz factor when viewed in the moving frame. Given that we could have placed the clock and the reflector at any two points in space, we conclude that a stationary and a moving observer will not agree on
measurements of lengths orientated parallel to their
relative motion. In fact, all such lengths will appear contracted by the Lorentz factor to the moving observer. This
effect is known as length contraction, and is equivalent to the Lorentz-Fitzgerald contraction discussed
in Section 3.1.6.