Kennedy-Thorndike Experiment
Suppose that we were to perform a version of the Michelson-Morley experiment in which the two
legs of the apparatus are of unequal (uncontracted) lengths  and
and 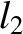 . Taking length contraction into account, the
time required for light to traverse the first leg of the apparatus is
. Taking length contraction into account, the
time required for light to traverse the first leg of the apparatus is
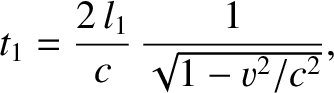 |
(3.62) |
where  is the speed of the laboratory with respect to the aether rest frame. Likewise, the time required for
light to traverse the second leg of the apparatus is
is the speed of the laboratory with respect to the aether rest frame. Likewise, the time required for
light to traverse the second leg of the apparatus is
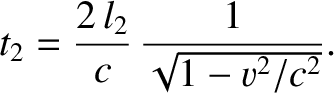 |
(3.63) |
Hence, the difference between these two times is
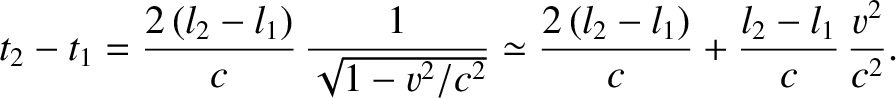 |
(3.64) |
Note that the time difference depends on  . Suppose that the laboratory is located on the Earth's
equator. In this case, the actual speed of the laboratory with respect to the aether rest frame varies
from
. Suppose that the laboratory is located on the Earth's
equator. In this case, the actual speed of the laboratory with respect to the aether rest frame varies
from
 to
to
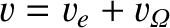 , throughout the course of a day, where
, throughout the course of a day, where
 is the Earth's mean orbital velocity, specified in Equation (3.20),
whereas
is the Earth's mean orbital velocity, specified in Equation (3.20),
whereas
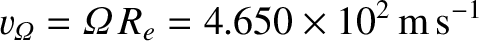 |
(3.65) |
is the speed of the Earth's surface due its axial rotation. Here,
 is the Earth's diurnal angular velocity [see Equation (1.351)], and
is the Earth's diurnal angular velocity [see Equation (1.351)], and
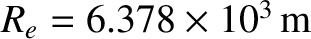 its equatorial radius. Thus,
its equatorial radius. Thus,  varies by about 3% during the course of the
day. This variation leads to a variation in the time difference, (3.64), that should be easily measurable.
However, when Roy Kennedy and Edward Thorndike performed this experiment in 1932 they observed no variation
in the time difference.
varies by about 3% during the course of the
day. This variation leads to a variation in the time difference, (3.64), that should be easily measurable.
However, when Roy Kennedy and Edward Thorndike performed this experiment in 1932 they observed no variation
in the time difference.
 and
and 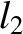 . Taking length contraction into account, the
time required for light to traverse the first leg of the apparatus is
. Taking length contraction into account, the
time required for light to traverse the first leg of the apparatus is
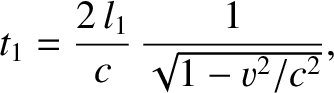
 is the speed of the laboratory with respect to the aether rest frame. Likewise, the time required for
light to traverse the second leg of the apparatus is
is the speed of the laboratory with respect to the aether rest frame. Likewise, the time required for
light to traverse the second leg of the apparatus is
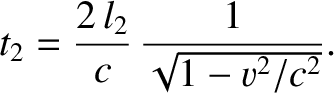
 . Suppose that the laboratory is located on the Earth's
equator. In this case, the actual speed of the laboratory with respect to the aether rest frame varies
from
. Suppose that the laboratory is located on the Earth's
equator. In this case, the actual speed of the laboratory with respect to the aether rest frame varies
from
 to
to
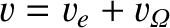 , throughout the course of a day, where
, throughout the course of a day, where
 is the Earth's mean orbital velocity, specified in Equation (3.20),
whereas
is the Earth's mean orbital velocity, specified in Equation (3.20),
whereas
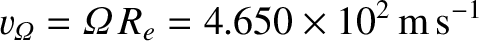
 is the Earth's diurnal angular velocity [see Equation (1.351)], and
is the Earth's diurnal angular velocity [see Equation (1.351)], and
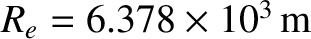 its equatorial radius. Thus,
its equatorial radius. Thus,  varies by about 3% during the course of the
day. This variation leads to a variation in the time difference, (3.64), that should be easily measurable.
However, when Roy Kennedy and Edward Thorndike performed this experiment in 1932 they observed no variation
in the time difference.
varies by about 3% during the course of the
day. This variation leads to a variation in the time difference, (3.64), that should be easily measurable.
However, when Roy Kennedy and Edward Thorndike performed this experiment in 1932 they observed no variation
in the time difference.