Aberration of Starlight and Stellar Parallax
Prior to the 20th century, one of the strongest arguments in favor of the existence of the aether was thought to be
the aberration of light. This is a phenomenon that produces an apparent motion of distant stars about their true positions, due to a combination of the finite velocity of light and the Earth's orbital motion about the Sun. Aberration is
closely related to another phenomenon, known as parallax, that also produces an apparent motion of distant stars about their true positions; in this case, due to the Earth's shifting position about the Sun. It is convenient to discuss these two effects together.
Figure 3.3:
Orbital motion of the Earth about the Sun.
|
|
The Earth moves around the Sun in a planar orbit whose plane includes the Sun. (See Section 1.9.2.)
The orbit is approximately circular in shape, and has a radius
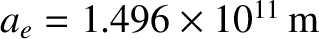 .
(See Sections 1.9.6, and Table 1.4.)
The plane that contains the Earth's orbit is known as the ecliptic plane. (See
Section 1.10.6.) Let us set up a Cartesian coordinate system in the ecliptic plane whose origin coincides with the
Sun, whose
.
(See Sections 1.9.6, and Table 1.4.)
The plane that contains the Earth's orbit is known as the ecliptic plane. (See
Section 1.10.6.) Let us set up a Cartesian coordinate system in the ecliptic plane whose origin coincides with the
Sun, whose  -axis is directed toward the northern ecliptic pole (i.e., the direction that is normal to the ecliptic plane in a northern sense), and whose
-axis is directed toward the northern ecliptic pole (i.e., the direction that is normal to the ecliptic plane in a northern sense), and whose  -axis is directed toward
the vernal equinox (i.e., the point in the sky at which the Sun annually passes through the projection of the Earth's equatorial
plane in a northward sense). See Figure 3.3. The angle,
-axis is directed toward
the vernal equinox (i.e., the point in the sky at which the Sun annually passes through the projection of the Earth's equatorial
plane in a northward sense). See Figure 3.3. The angle, 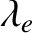 , shown in the figure, is known as the Earth's ecliptic
longitude, and serves to locate the Earth on its orbit. Let
, shown in the figure, is known as the Earth's ecliptic
longitude, and serves to locate the Earth on its orbit. Let 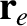 be the displacement of the Earth from the Sun.
It is clear from simple geometry that the components of
be the displacement of the Earth from the Sun.
It is clear from simple geometry that the components of 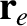 are
are
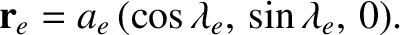 |
(3.13) |
Thus, the Earth's orbital velocity becomes
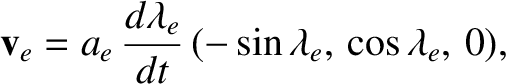 |
(3.14) |
where
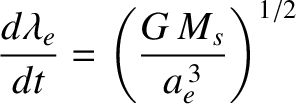 |
(3.15) |
is the Earth's mean orbital angular velocity about the Sun. (See Section 1.9.7.) Here,
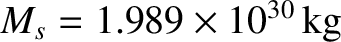 is the Sun's mass.
Let
is the Sun's mass.
Let 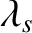 be the apparent ecliptic longitude of the Sun, as seen on the Earth. It is clear that
be the apparent ecliptic longitude of the Sun, as seen on the Earth. It is clear that
 . Hence, we deduce that
Here,
. Hence, we deduce that
Here, 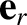 is a unit vector directed from the Earth to the Sun, whereas
is a unit vector directed from the Earth to the Sun, whereas
 is a unit vector that is
parallel to the Sun's apparent orbital velocity about the Earth. Finally,
is a unit vector that is
parallel to the Sun's apparent orbital velocity about the Earth. Finally,
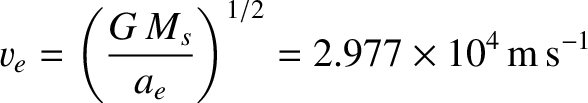 |
(3.20) |
is the Earth's mean orbital velocity about the Sun.
Figure 3.4:
Aberration of starlight.
|
|
Suppose that a light ray from a distant star is observed on the Earth. Let the phase velocity of the ray in the aether rest frame, in which the Sun is assumed to be stationary, be 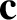 ,
where
,
where
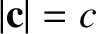 is the speed of light in vacuum. Because the Earth is actually moving with respect to the aether rest frame, the observed phase velocity of the light ray is
is the speed of light in vacuum. Because the Earth is actually moving with respect to the aether rest frame, the observed phase velocity of the light ray is
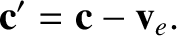 |
(3.21) |
[See Equation (3.12).]
Let  be the angle subtended between
be the angle subtended between 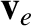 and
and 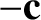 , and let
, and let  be the angle
subtended between
be the angle
subtended between 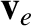 and
and 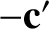 . See Figure 3.4. Thus,
. See Figure 3.4. Thus,  corresponds to the
true angular location of the star (i.e., the location seen by an observer in the Sun's rest frame), whereas
corresponds to the
true angular location of the star (i.e., the location seen by an observer in the Sun's rest frame), whereas  corresponds to the
apparent location of the star seen on the moving Earth. Simple trigonometry reveals that
corresponds to the
apparent location of the star seen on the moving Earth. Simple trigonometry reveals that
 |
(3.22) |
However,
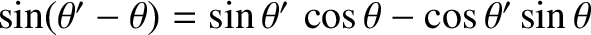 , so we get
, so we get
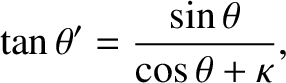 |
(3.23) |
where
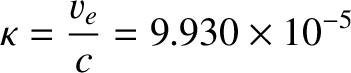 |
(3.24) |
is known as the constant of aberration.
Let us write
where the unit vectors 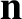 and
and 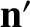 are directed toward the true position of the star (in the Sun's rest frame), and the apparent
position seen on the moving Earth, respectively. It is clear from Equations (3.17), (3.21), and (3.24)
that
to first order in
are directed toward the true position of the star (in the Sun's rest frame), and the apparent
position seen on the moving Earth, respectively. It is clear from Equations (3.17), (3.21), and (3.24)
that
to first order in 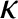 .
Let us write
Here,
.
Let us write
Here, 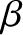 and
and 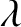 are the true ecliptic latitude and ecliptic longitude of the star,
respectively, whereas
are the true ecliptic latitude and ecliptic longitude of the star,
respectively, whereas 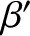 and
and 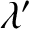 are the apparent latitude and longitude seen on the moving Earth.
(Ecliptic latitude and longitude parameterize position on the celestial sphere, and are similar to terrestrial latitude and longitude, except that the equator corresponds to the
Earth's orbital plane, and ecliptic longitude increases in the opposite direction to terrestrial longitude.)
It is clear from Equations (3.19) and (3.28) that
are the apparent latitude and longitude seen on the moving Earth.
(Ecliptic latitude and longitude parameterize position on the celestial sphere, and are similar to terrestrial latitude and longitude, except that the equator corresponds to the
Earth's orbital plane, and ecliptic longitude increases in the opposite direction to terrestrial longitude.)
It is clear from Equations (3.19) and (3.28) that
 |
(3.30) |
Hence, Equations (3.27)–(3.29) yield
Equations (3.31) and (3.32) can be combined to give
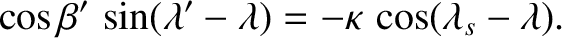 |
(3.34) |
Finally, writing
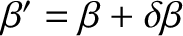 and
and
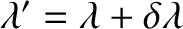 , Equations (3.33)
and (3.34) yield
to first order in
, Equations (3.33)
and (3.34) yield
to first order in 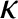 .
If
.
If
 represents angular displacement on the celestial sphere in a direction parallel to the
ecliptic plane (in the sense of the Sun's apparent motion with respect to the stars), and
represents angular displacement on the celestial sphere in a direction parallel to the
ecliptic plane (in the sense of the Sun's apparent motion with respect to the stars), and
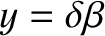 represents
angular displacement in a direction perpendicular to the ecliptic (in a northern sense), then the previous
two equations give
This is clearly the parametric equation of an ellipse. Hence, we deduce that, as a consequence of the aberration of light, during the course of a year, our star
appears to describe an ellipse on the celestial sphere. The major radius,
represents
angular displacement in a direction perpendicular to the ecliptic (in a northern sense), then the previous
two equations give
This is clearly the parametric equation of an ellipse. Hence, we deduce that, as a consequence of the aberration of light, during the course of a year, our star
appears to describe an ellipse on the celestial sphere. The major radius, 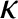 , is parallel to the
ecliptic plane, whereas the minor radius,
, is parallel to the
ecliptic plane, whereas the minor radius,
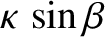 , is perpendicular to the ecliptic. The angular displacement of the star from its mean position is
greatest when
, is perpendicular to the ecliptic. The angular displacement of the star from its mean position is
greatest when
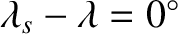 , or
, or 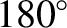 (i.e., when the ecliptic longitude of the star matches
that of the Sun, or differs from it by
(i.e., when the ecliptic longitude of the star matches
that of the Sun, or differs from it by 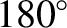 , which maximizes the Earth's transverse velocity with respect to the star). The magnitude of the greatest angular displacement,
, which maximizes the Earth's transverse velocity with respect to the star). The magnitude of the greatest angular displacement, 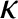 , is
, is  arc seconds. This is about the same as the angular size of Saturn's disk.
arc seconds. This is about the same as the angular size of Saturn's disk.
Figure 3.5:
Stellar parallax.
|
|
Let us now consider parallax. Let 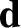 be the displacement of the Sun from a distant star, let
be the displacement of the Sun from a distant star, let
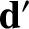 be the corresponding displacement of the Earth, and let
be the corresponding displacement of the Earth, and let 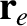 be the displacement of the
Earth from the Sun. It is evident that
be the displacement of the
Earth from the Sun. It is evident that
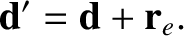 |
(3.39) |
See Figure 3.5. Let  be the angle subtended between
be the angle subtended between 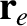 and
and  , and let
, and let  be the angle
subtended between
be the angle
subtended between 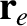 and
and 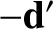 . Thus,
. Thus,  corresponds to the
true location of the star (i.e., the location seen by an observer on the Sun), whereas
corresponds to the
true location of the star (i.e., the location seen by an observer on the Sun), whereas  corresponds to the
apparent location of the star seen on the displaced Earth. Simple trigonometry reveals that
corresponds to the
apparent location of the star seen on the displaced Earth. Simple trigonometry reveals that
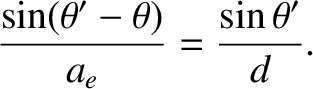 |
(3.40) |
However,
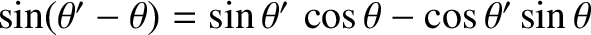 , so we get
, so we get
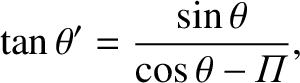 |
(3.41) |
where
 |
(3.42) |
is known as the star's parallax. If we measure the star's distance from the Sun, 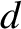 , in units of
parsecs (pc) then, by definition, the parallax in arc seconds is
, in units of
parsecs (pc) then, by definition, the parallax in arc seconds is
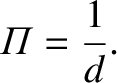 |
(3.43) |
It follows that
 |
(3.44) |
Given that the nearest star to the Sun, Proxima Centauri, is 1.302 parsecs away, it is clear that all stellar
parallaxes are less than 1 arc second. This implies that stellar aberration is a much larger effect than stellar parallax.
We can write
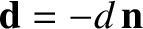 and
and
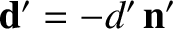 . Making use of very similar analysis to that used to calculate
aberration, we obtain
. Making use of very similar analysis to that used to calculate
aberration, we obtain
Equations (3.47) and (3.48) can be combined to give
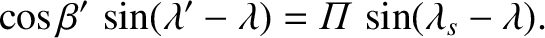 |
(3.50) |
Hence, Equations (3.49) and (3.50) yield
to first order in 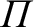 .
If we again let
.
If we again let
 represent angular displacement on the celestial sphere in a direction parallel to the
ecliptic plane, and
represent angular displacement on the celestial sphere in a direction parallel to the
ecliptic plane, and
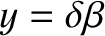 represent
angular displacement in a direction perpendicular to the ecliptic, then the previous
two equations give
This is again the parametric equation of an ellipse. Hence, we deduce that, as a consequence parallax, during the course of a year, our star
appears to describe an ellipse on the celestial sphere. The major radius,
represent
angular displacement in a direction perpendicular to the ecliptic, then the previous
two equations give
This is again the parametric equation of an ellipse. Hence, we deduce that, as a consequence parallax, during the course of a year, our star
appears to describe an ellipse on the celestial sphere. The major radius, 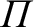 , is parallel to the
ecliptic plane, whereas the minor radius,
, is parallel to the
ecliptic plane, whereas the minor radius,
 , is perpendicular to the ecliptic. The angular displacement of the star from its mean position is
greatest when
, is perpendicular to the ecliptic. The angular displacement of the star from its mean position is
greatest when
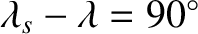 , or
, or 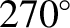 (i.e., when the ecliptic longitude of the star differs from
that of the Sun by
(i.e., when the ecliptic longitude of the star differs from
that of the Sun by 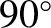 or
or 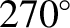 , which maximizes the Earth's transverse displacement with respect to the star). The greatest angular displacement,
, which maximizes the Earth's transverse displacement with respect to the star). The greatest angular displacement, 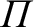 , when measured in arc seconds, is
equal to one over the distance of the star from the Sun measured in parsecs. [See Equation (3.43).]
, when measured in arc seconds, is
equal to one over the distance of the star from the Sun measured in parsecs. [See Equation (3.43).]
Between 1725 and 1727, the astronomers James Bradley and Samuel Molyneux measured the position of the
circumpolar star  Draconis in an attempt to observe its parallax. They found that the angular position
of the star underwent small annual variations, but that the deviation from the mean was greatest when the ecliptic
longitude of the Sun matched that of the star, which is not the behavior expected from parallax. In 1728, Bradley
correctly explained the observed variations in terms of the aberration of light. Note that this explanation depends
crucially on the fact that the speed of light observed in a frame of reference that moves with respect to the
rest frame of the aether is different to that observed in the rest frame. Incidentally, stellar parallax is so small an effect
that it was not successfully measured until 1838, when Frederich Bessel measured the parallax of the star 61 Cygni.
Draconis in an attempt to observe its parallax. They found that the angular position
of the star underwent small annual variations, but that the deviation from the mean was greatest when the ecliptic
longitude of the Sun matched that of the star, which is not the behavior expected from parallax. In 1728, Bradley
correctly explained the observed variations in terms of the aberration of light. Note that this explanation depends
crucially on the fact that the speed of light observed in a frame of reference that moves with respect to the
rest frame of the aether is different to that observed in the rest frame. Incidentally, stellar parallax is so small an effect
that it was not successfully measured until 1838, when Frederich Bessel measured the parallax of the star 61 Cygni.
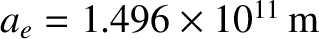 .
(See Sections 1.9.6, and Table 1.4.)
The plane that contains the Earth's orbit is known as the ecliptic plane. (See
Section 1.10.6.) Let us set up a Cartesian coordinate system in the ecliptic plane whose origin coincides with the
Sun, whose
.
(See Sections 1.9.6, and Table 1.4.)
The plane that contains the Earth's orbit is known as the ecliptic plane. (See
Section 1.10.6.) Let us set up a Cartesian coordinate system in the ecliptic plane whose origin coincides with the
Sun, whose  -axis is directed toward the northern ecliptic pole (i.e., the direction that is normal to the ecliptic plane in a northern sense), and whose
-axis is directed toward the northern ecliptic pole (i.e., the direction that is normal to the ecliptic plane in a northern sense), and whose  -axis is directed toward
the vernal equinox (i.e., the point in the sky at which the Sun annually passes through the projection of the Earth's equatorial
plane in a northward sense). See Figure 3.3. The angle,
-axis is directed toward
the vernal equinox (i.e., the point in the sky at which the Sun annually passes through the projection of the Earth's equatorial
plane in a northward sense). See Figure 3.3. The angle, 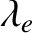 , shown in the figure, is known as the Earth's ecliptic
longitude, and serves to locate the Earth on its orbit. Let
, shown in the figure, is known as the Earth's ecliptic
longitude, and serves to locate the Earth on its orbit. Let 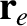 be the displacement of the Earth from the Sun.
It is clear from simple geometry that the components of
be the displacement of the Earth from the Sun.
It is clear from simple geometry that the components of 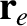 are
are
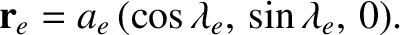
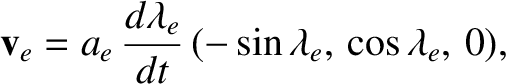
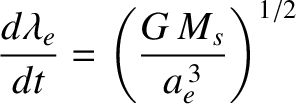
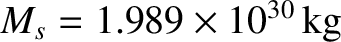 is the Sun's mass.
Let
is the Sun's mass.
Let  be the apparent ecliptic longitude of the Sun, as seen on the Earth. It is clear that
be the apparent ecliptic longitude of the Sun, as seen on the Earth. It is clear that
 . Hence, we deduce that
Here,
. Hence, we deduce that
Here, 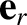 is a unit vector directed from the Earth to the Sun, whereas
is a unit vector directed from the Earth to the Sun, whereas
 is a unit vector that is
parallel to the Sun's apparent orbital velocity about the Earth. Finally,
is the Earth's mean orbital velocity about the Sun.
is a unit vector that is
parallel to the Sun's apparent orbital velocity about the Earth. Finally,
is the Earth's mean orbital velocity about the Sun.
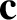 ,
where
,
where
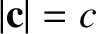 is the speed of light in vacuum. Because the Earth is actually moving with respect to the aether rest frame, the observed phase velocity of the light ray is
is the speed of light in vacuum. Because the Earth is actually moving with respect to the aether rest frame, the observed phase velocity of the light ray is
 be the angle subtended between
be the angle subtended between 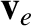 and
and 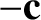 , and let
, and let  be the angle
subtended between
be the angle
subtended between 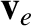 and
and 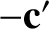 . See Figure 3.4. Thus,
. See Figure 3.4. Thus,  corresponds to the
true angular location of the star (i.e., the location seen by an observer in the Sun's rest frame), whereas
corresponds to the
true angular location of the star (i.e., the location seen by an observer in the Sun's rest frame), whereas  corresponds to the
apparent location of the star seen on the moving Earth. Simple trigonometry reveals that
corresponds to the
apparent location of the star seen on the moving Earth. Simple trigonometry reveals that

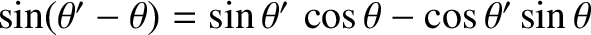 , so we get
where
is known as the constant of aberration.
, so we get
where
is known as the constant of aberration.
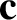
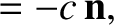
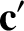
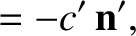
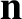 and
and 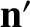 are directed toward the true position of the star (in the Sun's rest frame), and the apparent
position seen on the moving Earth, respectively. It is clear from Equations (3.17), (3.21), and (3.24)
that
to first order in
are directed toward the true position of the star (in the Sun's rest frame), and the apparent
position seen on the moving Earth, respectively. It is clear from Equations (3.17), (3.21), and (3.24)
that
to first order in 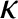 .
Let us write
Here,
.
Let us write
Here, 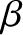 and
and 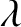 are the true ecliptic latitude and ecliptic longitude of the star,
respectively, whereas
are the true ecliptic latitude and ecliptic longitude of the star,
respectively, whereas 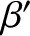 and
and 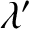 are the apparent latitude and longitude seen on the moving Earth.
(Ecliptic latitude and longitude parameterize position on the celestial sphere, and are similar to terrestrial latitude and longitude, except that the equator corresponds to the
Earth's orbital plane, and ecliptic longitude increases in the opposite direction to terrestrial longitude.)
It is clear from Equations (3.19) and (3.28) that
are the apparent latitude and longitude seen on the moving Earth.
(Ecliptic latitude and longitude parameterize position on the celestial sphere, and are similar to terrestrial latitude and longitude, except that the equator corresponds to the
Earth's orbital plane, and ecliptic longitude increases in the opposite direction to terrestrial longitude.)
It is clear from Equations (3.19) and (3.28) that

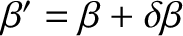 and
and
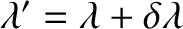 , Equations (3.33)
and (3.34) yield
, Equations (3.33)
and (3.34) yield
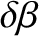

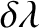
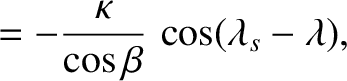
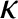 .
If
.
If
 represents angular displacement on the celestial sphere in a direction parallel to the
ecliptic plane (in the sense of the Sun's apparent motion with respect to the stars), and
represents angular displacement on the celestial sphere in a direction parallel to the
ecliptic plane (in the sense of the Sun's apparent motion with respect to the stars), and
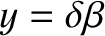 represents
angular displacement in a direction perpendicular to the ecliptic (in a northern sense), then the previous
two equations give
represents
angular displacement in a direction perpendicular to the ecliptic (in a northern sense), then the previous
two equations give
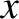
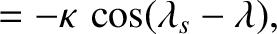
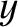
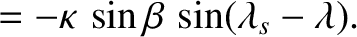
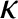 , is parallel to the
ecliptic plane, whereas the minor radius,
, is parallel to the
ecliptic plane, whereas the minor radius,
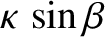 , is perpendicular to the ecliptic. The angular displacement of the star from its mean position is
greatest when
, is perpendicular to the ecliptic. The angular displacement of the star from its mean position is
greatest when
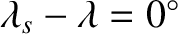 , or
, or 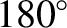 (i.e., when the ecliptic longitude of the star matches
that of the Sun, or differs from it by
(i.e., when the ecliptic longitude of the star matches
that of the Sun, or differs from it by 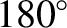 , which maximizes the Earth's transverse velocity with respect to the star). The magnitude of the greatest angular displacement,
, which maximizes the Earth's transverse velocity with respect to the star). The magnitude of the greatest angular displacement, 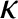 , is
, is  arc seconds. This is about the same as the angular size of Saturn's disk.
arc seconds. This is about the same as the angular size of Saturn's disk.
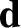 be the displacement of the Sun from a distant star, let
be the displacement of the Sun from a distant star, let
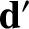 be the corresponding displacement of the Earth, and let
be the corresponding displacement of the Earth, and let 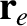 be the displacement of the
Earth from the Sun. It is evident that
be the displacement of the
Earth from the Sun. It is evident that
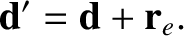
 be the angle subtended between
be the angle subtended between 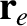 and
and  , and let
, and let  be the angle
subtended between
be the angle
subtended between 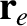 and
and 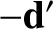 . Thus,
. Thus,  corresponds to the
true location of the star (i.e., the location seen by an observer on the Sun), whereas
corresponds to the
true location of the star (i.e., the location seen by an observer on the Sun), whereas  corresponds to the
apparent location of the star seen on the displaced Earth. Simple trigonometry reveals that
corresponds to the
apparent location of the star seen on the displaced Earth. Simple trigonometry reveals that
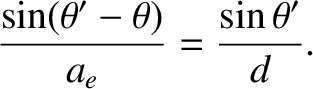
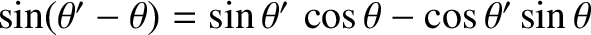 , so we get
, so we get
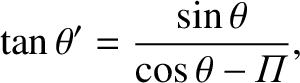
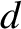 , in units of
parsecs (pc) then, by definition, the parallax in arc seconds is
It follows that
, in units of
parsecs (pc) then, by definition, the parallax in arc seconds is
It follows that

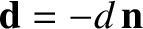 and
and
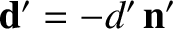 . Making use of very similar analysis to that used to calculate
aberration, we obtain
. Making use of very similar analysis to that used to calculate
aberration, we obtain
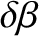
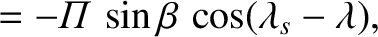
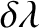
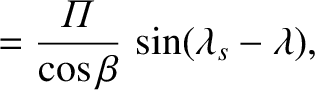
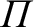 .
If we again let
.
If we again let
 represent angular displacement on the celestial sphere in a direction parallel to the
ecliptic plane, and
represent angular displacement on the celestial sphere in a direction parallel to the
ecliptic plane, and
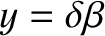 represent
angular displacement in a direction perpendicular to the ecliptic, then the previous
two equations give
represent
angular displacement in a direction perpendicular to the ecliptic, then the previous
two equations give
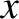
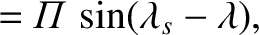
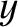
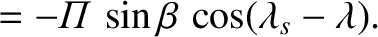
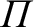 , is parallel to the
ecliptic plane, whereas the minor radius,
, is parallel to the
ecliptic plane, whereas the minor radius,
 , is perpendicular to the ecliptic. The angular displacement of the star from its mean position is
greatest when
, is perpendicular to the ecliptic. The angular displacement of the star from its mean position is
greatest when
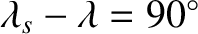 , or
, or 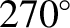 (i.e., when the ecliptic longitude of the star differs from
that of the Sun by
(i.e., when the ecliptic longitude of the star differs from
that of the Sun by 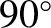 or
or 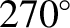 , which maximizes the Earth's transverse displacement with respect to the star). The greatest angular displacement,
, which maximizes the Earth's transverse displacement with respect to the star). The greatest angular displacement, 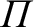 , when measured in arc seconds, is
equal to one over the distance of the star from the Sun measured in parsecs. [See Equation (3.43).]
, when measured in arc seconds, is
equal to one over the distance of the star from the Sun measured in parsecs. [See Equation (3.43).]
 Draconis in an attempt to observe its parallax. They found that the angular position
of the star underwent small annual variations, but that the deviation from the mean was greatest when the ecliptic
longitude of the Sun matched that of the star, which is not the behavior expected from parallax. In 1728, Bradley
correctly explained the observed variations in terms of the aberration of light. Note that this explanation depends
crucially on the fact that the speed of light observed in a frame of reference that moves with respect to the
rest frame of the aether is different to that observed in the rest frame. Incidentally, stellar parallax is so small an effect
that it was not successfully measured until 1838, when Frederich Bessel measured the parallax of the star 61 Cygni.
Draconis in an attempt to observe its parallax. They found that the angular position
of the star underwent small annual variations, but that the deviation from the mean was greatest when the ecliptic
longitude of the Sun matched that of the star, which is not the behavior expected from parallax. In 1728, Bradley
correctly explained the observed variations in terms of the aberration of light. Note that this explanation depends
crucially on the fact that the speed of light observed in a frame of reference that moves with respect to the
rest frame of the aether is different to that observed in the rest frame. Incidentally, stellar parallax is so small an effect
that it was not successfully measured until 1838, when Frederich Bessel measured the parallax of the star 61 Cygni.